УДК 621.38:622.276.34:531.746

Г.И.Чесноков, канд. техн. наук, В.И.Галкин, канд. техн. наук, Д.В.Галкин, канд. техн. наук,

АООТ “Московский институт электромеханики и автоматики”

КОНТРОЛЬ ПРОСТРАНСТВЕННОЙ ОРИЕНТАЦИИ СТВОЛОВ СКВАЖИН ГИРОСКОПИЧЕСКИМ МЕТОДОМ

Представлены алгоритмы определения углов пространственной ориентации скважины в процессе движения измерительного блока гироскопического инклинометра бесплатформенного типа. Рассмотрены и проанализированы различные способы построения кинематических уравнений на предмет минимизации времени, затрачиваемого на их решение. Показан рабочий алгоритм наиболее перспективного многошагового построения с использованием параметров Родрига-Гамильтона в кватернионной форме записи угловых поворотов измерительного блока

Введение

Исходные положения

Представление кинематических уравнений через измеряемые углы

Определение углов ориентации скважины через направляющие косинусы

Определение углов ориентации скважины через параметры Родрига-Гамильтона

Выводы

Введение

Применение гироскопических инклинометров для определения пространственной ориентации скважин в нефтегазодобывающей промышленности позволяет осуществлять строительство скважин в условиях магнитных аномалий с использованием обсадных труб из магнитомягких материалов. Это существенно расширяет возможности промышленной добычи нефти и газа, снижает затраты на строительство скважин.

АООТ “Московский институт электромеханики и автоматики” (АООТ “МИЭА”), используя свой научно-технический потенциал по созданию инерциальных навигационных систем для аэрокосмической отрасли, разрабатывает малогабаритные высокоточные гироскопические инклинометры бесплатформенного типа [1,2], позволяющие реализовать наиболее эффективные способы построения скважин на основе кустового, наклонного и горизонтального бурения. Примером таких разработок является гироскопический инклинометр “ГИД” [2], измерительный блок которого представлен на рис. 1.

Рис. 1. Измерительный блок гироскопического
инклинометра “ГИД”

Важнейшей технической характеристикой современных инклинометров является оперативность получения и обработки информации. Разрабатываемые в АООТ “МИЭА” гироскопические инклинометры позволяют определять угловое положение скважины в процессе движения измерительного блока, что приводит к максимальному сокращению времени промера скважины. Достигается это за счет использования специальных расчетных алгоритмов. Ниже изложены особенности разработанных алгоритмов, показаны различные варианты их реализации.

Исходные положения

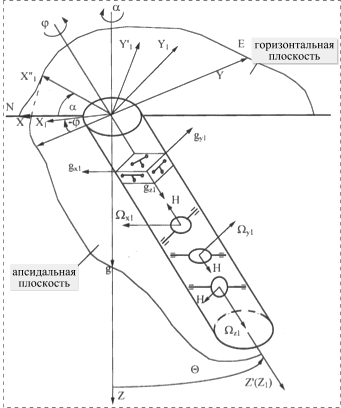
Измерительный блок гироскопического инклинометра бесплатформенного типа в общем случае состоит из трех двухстепенных гироскопов, работающих в режиме датчиков угловых скоростей (ДУС), и трех линейных акселерометров. На рис. 2 показана структурная схема измерительного блока и система координат, используемая для определения углового положения ствола скважины. Местоположение измерительного блока в скважине определяется по длине каротажного кабеля.

Рис. 2. Расчетная система координат

В качестве базовой системы координат, относительно которой определяется угловое положение скважины, принят географический сопровождающий трехгранник , в котором ось направлена по местной вертикали к центру Земли, ось лежит в плоскости горизонта и направлена на север, а ось направлена на восток.

Угловое положение оси ствола скважины в точке ее замера, задаваемое системой координат определяется двумя углами: зенитным углом – углом отклонения ствола скважины относительно местной вертикали и азимутальным углом – углом отклонения апсидальной плоскости ствола скважины от плоскости местного меридиана.

Система координат измерительного блока , , связана с осями чувствительности гироскопов и акселерометров. В расчетах принято, что одноименные оси чувствительности гироскопов и акселерометров совпадают друг с другом и лежат в точке измерения положения оси ствола скважины .

Основной особенностью определения пространственной ориентации скважины с помощью бесплатформенного измерительного блока является отсутствие жесткой связи между измерительным блоком и скважиной, т.е. измерительный блок может поворачиваться вокруг оси скважины на угол . Этот угол в геодезии принято называть углом установки отклонителя или углом поворота инклинометра.

Для определения углового положения скважины в процессе движения измерительного блока разработаны кинематические уравнения, учитывающие вышеуказанную особенность. При этом принято допущение, что скоростью движения измерительного блока, перпендикулярной местной вертикали, можно пренебречь. Исследовано несколько способов представления кинематических уравнений: через измеряемые углы, через направляющие косинусы, через параметры Родрига-Гамильтона.

Представление кинематических уравнений через измеряемые углы

Такое представление уравнений является наиболее простым и очевидным. Используя принятые системы координат и находя проекции векторов угловых скоростей на измерительные оси трехгранника при его поворотах относительно базового трехгранника на интересующие нас углы , , (рис. 1), получим три дифференциальных уравнения [3]:

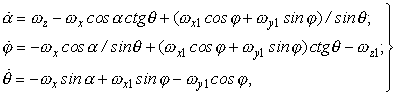(2.1)

где , , – проекции угловой скорости вращения измерительного трехгранника в инерциальном пространстве, измеряемые гироскопами; – горизонтальная составляющая скорости вращения Земли; – вертикальная составляющая скорости вращения Земли; – угловая скорость вращения Земли; – широта местности в точке замера скважины.

Решая полученные уравнения относительно , и , найдем искомые углы ориентации скважины и инклинометра. Однако, несмотря на кажущуюся простоту полученных уравнений, их решение представляет собой весьма трудоемкую задачу из-за нелинейности уравнений, необходимости в каждый момент времени определять тригонометрические функции, из-за неопределенности решений при , равном нулю.

В теории бесплатформенных инерциальных систем, к которым относится и рассматриваемый инклинометр, наибольшее распространение получили кинематические уравнения, использующие методы направляющих косинусов и параметры Родрига-Гамильтона. Получаемые при этом уравнения линейны и не вырождаются ни при каких углах поворота инклинометра.

Определение углов ориентации скважины через направляющие косинусы

В этом случае запись кинематических уравнений осуществляется через матрицу направляющих косинусов, которая связывает угловое положение измерительного трехгранника относительно сопровождающего географического трехгранника следующим образом:

, (3.1)

где – матрица направляющих косинусов, записываемая для рассматриваемого случая в следующем виде [4]:

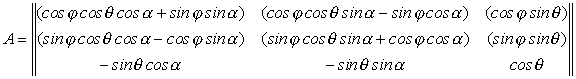, (3.2)

или через ее элементы:

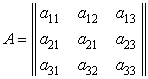. (3.3)

Как видно из (3.2), (3.3), зная элементы матрицы , углы наклона скважины и угол поворота инклинометра легко определить из следующих соотношений:

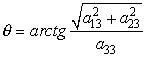; ; . (3.4)

При поворотах измерительного трехгранника относительно сопровождающего трехгранника в результате движения измерительного блока внутри скважины элементы матрицы являются функциями времени . Естественно, функциями времени являются и определяемые углы , , .

Связь матрицы направляющих косинусов с вектором скорости вращения измерительного трехгранника относительно географического сопровождающего трехгранника устанавливается кинематическим уравнением Пуассона [5]:

, (3.5)

где – матрица направляющих косинусов в функции времени; – кососимметричная матрица вектора угловой скорости вращения измерительного трехгранника относительно сопровождающего трехгранника .

Поскольку гироскопы измеряют абсолютную угловую скорость измерительного блока в инерциальном пространстве, то выражение (3.5) удобнее записать в виде:

, (3.6)

где – кососимметричная матрица абсолютной угловой скорости вращения измерительного трехгранника в инерциальном пространстве; – кососимметричная матрица абсолютной угловой скорости вращения географического сопровождающего трехгранника в инерциальном пространстве, определяемая при принятых допущениях скоростью вращения Земли.

Матричное уравнение (3.6) содержит девять скалярных дифференциальных уравнений:

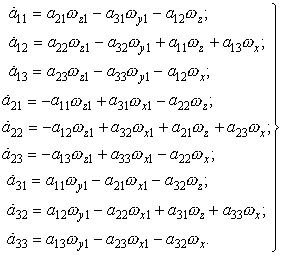(3.7)

Значения угловых скоростей , , определяются по показаниям гироскопов, а , являются горизонтальной и вертикальной составляющими скорости вращения Земли. Решая полученную систему уравнений (3.7) численными методами, находим значения элементов матрицы в каждый момент времени, а по ним, используя соотношения (3.4), – и искомые углы ориентации скважины.

Недостатками такого способа решения задачи является большой объем вычислений, что накладывает ограничения на скорость обработки информации в реальном масштабе времени. Более эффективным в этом отношении является использование параметров Родрига-Гамильтона.

Определение углов ориентации скважины через параметры Родрига-Гамильтона

Кинематические уравнения движения измерительного блока в этом случае записываются в кватернионной форме [6]:

, (4.1)

где – кватернион, описывающий поворот измерительного трехгранника относительно базового сопровождающего трехгранника :

, (4.2)

, , , – параметры Родрига-Гамильтона; – вектор угловой скорости трехгранника относительно трехгранника .

Так как гироскопы измеряют абсолютную угловую скорость трехгранника в инерциальном пространстве, то результирующий кватернион следует записать в виде произведения двух кватернионов: – кватерниона поворота измерительного трехгранника в инерциальном пространстве и – кватерниона поворота географического сопровождающего трехгранника в этом же пространстве:

. (4.3)

Способ нахождения и , а следовательно и , зависят от формы представления первичной информации – в виде угловых скоростей или в виде квазикоординат. Рассмотрим оба эти случая.

При представлении первичной информации в виде угловых скоростей для определения кватернионов и и соответствующих им параметров Родрига-Гамильтона необходимо решить частные кинематические уравнения:

; . (4.4)

В скалярном виде эти уравнения запишутся следующим образом:

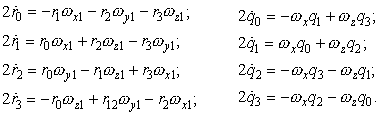(4.5)

Решение этих уравнений позволит найти значения параметров Родрига-Гамильтона , , , и , , , , а через них, используя соотношение (4.3), – и значения , , , , необходимые для определения элементов матрицы направляющих косинусов:

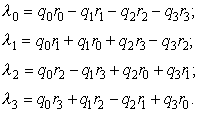(4.6)

В ряде случаев информация с датчиков угловых скоростей выдается в форме так называемых квазикоординат:

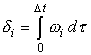, (4.7)

где – угловая скорость измерительного блока; - временной интервал интегрирования ; – квазикоордината углового поворота измерительного блока за время .

В этом случае кватернионы удобнее находить через приращение вектора истинного поворота . Расчет вектора истинного поворота выполняют через квазикоординаты в одношаговом или многошаговом режимах. В одношаговом режиме приращение вектора истинного поворота эквивалентно квазикоординате за рассматриваемый интервал времени. В более точном многошаговом режиме, когда приращение вектора истинного поворота определяется за несколько шагов измерений, его связь с квазикоординатами имеет более сложную форму [7]. Например, для четырехшагового режима она имеет вид:

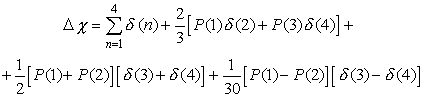. (4.8)

где ; ; – номер шагов; – кососимметричная матрица, элементами которой являются квазикоординаты:

. (4.9)

Для определения кватерниона через используется следующее выражение:

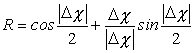, (4.10)

где ; , откуда параметры Родрига-Гамильтона определяются следующим образом:

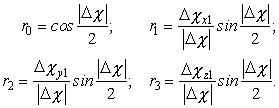(4.11)

Аналогичным образом находятся параметры Родрига-Гамильтона и для кватерниона . Параметры Родрига-Гамильтона результирующего кватерниона рассчитываются с помощью системы уравнений (4.6).

Зная параметры Родриго-Гамильтона результирующего кварерниона, значения элементов матрицы направляющих косинусов можно определить, используя известные соотношения [5]:

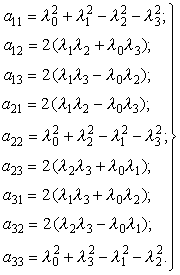(4.12)

По результатам вычислений , используя соотношение (3.4), находят искомые углы ориентации скважины и измерительного блока , , .

Исследования алгоритмов, основанных на использовании параметров Родрига-Гамильтона, показали, что с их помощью можно сократить время расчета углов ориентации скважины на (30-50) % по сравнению с матрицей направляющих косинусов, особенно при использовании квазикоординат, так как в этом случае отпадает необходимость решать дифференциальные уравнения.

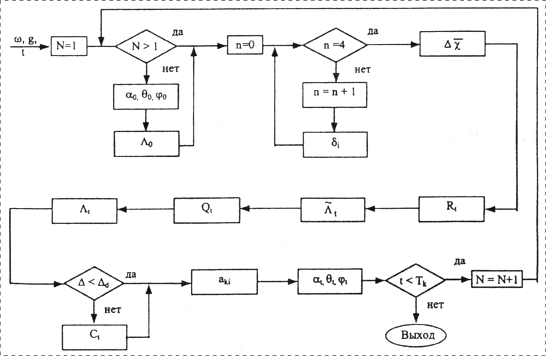
На рис. 3 в качестве примера показан рабочий четырехшаговый алгоритм, реализующий идею использования параметров Родрига-Гамильтона в кватернионной форме записи на базе представления первичной информации в виде квазикоординат. Он имеет ряд особенностей, обеспечивающих его практическую реализацию и необходимую точность расчетов.

Рис. 3. Структурная схема рабочего алгоритма

Перед запуском алгоритма необходимо определять начальный нулевой кватернион . Осуществляется это следующим образом. В режиме выставки, когда измерительный блок стоит неподвижно, рассчитываются начальные углы ориентации скважины , , . Для этого используется аналитическая связь (3.1) между показаниями гироскопов и акселерометров по измерительным осям и значениями проекций скорости вращения Земли и ускорения силы тяжести на базовые оси сопровождающего географического трехгранника . После соответствующих преобразований уравнения (3.1) с учетом (3.2) выражения для определения начальных углов ориентации могут быть представлены в следующем виде [4]:

; ;

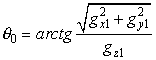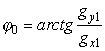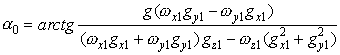. (4.13)

По начальным углам ориентации рассчитываются параметры Родрига-Гамильтона нулевого кватерниона , а затем и сам кватернион:

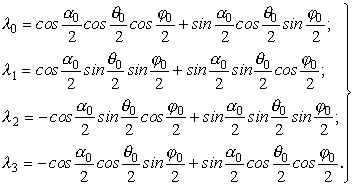(4.14)

С целью сведения к минимуму ошибок вычислений кватерниона , результирующего поворота определяется и учитывается отклонение нормы кватерниона от единицы:

. (4.15)

Полученное в результате расчетов значение сравнивается с допускаемым отклонением . Если , то в дальнейших расчетах используется кватернион . Если же , то определяется новый нормированный кватернион , который и используется в дальнейших расчетах при определении углов , , :

. (4.16)

В представленном алгоритме кватернион обновленного положения трехгранника является произведением кватерниона результирующего поворота трехгранника, полученного на предыдущем шаге измерений, на кватернион поворота трехгранника текущего шага измерений.

Выводы

1. Получены расчетные алгоритмы для определения углов пространственной ориентации скважины с помощью гироскопического инклинометра бесплатформенного типа в процессе движения его измерительного блока.

2. Исследования полученных алгоритмов показали, что наиболее перспективным с точки зрения скорости обработки информации является алгоритм, построенный на базе параметров Родрига-Гамильтона с представлением исходных для расчетов данных в виде квазикоординат

3. По мнению авторов, рассмотренные в настоящей статье алгоритмы представляют практический интерес не только для разработчиков гироскопических инклинометров бесплатформенного типа, но и для разработчиков бесплатформенных измерительных устройств иного назначения, когда при определении ориентации объекта измерительное устройство может свободно перемещаться внутри этого объекта.

Список литературы

1. А. с. № 1827541. Измерительный блок инклинометра / В.И.Галкин, Е.А.Измайлов, А.А.Маслов – Б. И. № 26, 1993.

2. Галкин В.И., Измайлов Е.А., Жилин В.Б., Суминов В.М., Галкин Д.В. Гироскопический инклинометр “ГИД” // Гироскопия и навигация. 1997. № 4. С. 26-33.

3. Галкин Д.В. Разработка и исследование информационно-вычислительной системы гироскопического инклинометра для диагностики и активного контроля пространственного положения ствола скважин: Автореф. дисс. на соиск. учен. ст. к.т.н. М: Моск. авиационно-технолог. ин-т РГТУ им К.Э.Циолковского, 1999. 26 с.

4. Суминов В.М., Галкин Д.В. Математическая модель метрологической системы гироскопического инклинометра // Научно-технический сборник “Стандартизация и унификация авиационной техники” М: НИИСУ, 1997. С. 39-47.

5. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М: Наука, 1976.

6. Бранен В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого тела. М: Наука. 1973.

7. Панов А.П. Математические основы теории инерциальной навигации. Киев. Наукова думка, 1995.

8. Чесноков Г.И., Галкин В.И., Галкин Д.В. Контроль пространственной ориентации стволов скважин гироскопическим инклинометром в процессе движения измерительного блока // Материалы VII Санкт-Петербургской международной конференции по интегрированным навигационным системам (29-21 мая, 2000 г) М, 2000. С. 51-59.

Наверх