И.А.Обухов, канд. физ.-мат. наук, ИМАШ РАН
МОДЕЛИРОВАНИЕ
СТАТИЧЕСКИХ ХАРАКТЕРИСТИК РЕЗОНАНСНО-ТУННЕЛЬНЫХ ПРИБОРОВ
![]()
|
Описаны модели, позволяющие рассчитывать статические характеристики квантовых приборов на основе резонансно-туннельных структур и получать результаты, близкие к экспериментальным |
Взаимодействие классических и
квантовых областей РТД
Введение
В настоящее время приборы, созданные на основе резонансно-туннельных структур (РТС), такие как резонансно-туннельные диоды (РТД), уже перестали быть экзотическими и находят постоянно расширяющуюся сферу применения в устройствах СВЧ и КВЧ диапазонов [1]. Практически промышленной является и технология производства этих приборов.
Однако далеко не все проблемы, с которыми столкнулись разработчики первых РТС, решены до конца. Некоторые из них касаются не только собственного РТС, но являются отражением общих проблем понимания принципов функционирования квантовых приборов и, по-видимому, решение их будет актуальным еще длительное время.
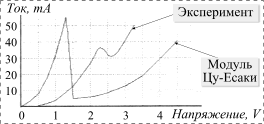
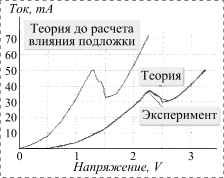
К таковым относится и проблема адекватного описания статических характеристик приборов. Коротко, она состоит в том, что на основе простейших представлений квантовой механики и кинетической теории невозможно дать сколько-нибудь удовлетворительное описание вольт-амперных характеристик (ВАХ) приборов. Результаты расчетов и экспериментальные данные различаются в несколько раз, а часто и на целые порядки (рис. 1).
|
|
|
Рис. 1. Типичные экспериментальная и расчетная ВАХ для AlGаAs РТД на полуизолирующей подложке |
Анализ большого массива данных показывает, что подобная ситуация является типичной практически для всех общеизвестных моделей, с нею сталкивались и сталкиваются до сих пор все исследовательские группы во всех центрах.
В статье приведены результаты работы по построению модели переноса заряда, позволяющей решить некоторые из проблем адекватного описания ВАХ РТД и других квантовых приборов и достаточно долго использовавшейся для практических расчетов. Модель была разработана еще в период создания первых советских РТД (конец 80-х – начало 90-х годов) [2-4]. Работа была инициирована Ю.С.Тиходеевым, руководившим коллективом, создавшим первые в СССР РТД.
Прежде чем перейти к изложению модели, заметим, что адекватное описание характеристик квантовых приборов имеет, как минимум, две существенные составляющие:
1. Описание собственно квантового транспорта при ненулевых температурах.
2. Описание взаимодействия классических и квантовых областей приборов, функционирующих на квантовых принципах.
Ниже будут предложены возможные пути решения обеих этих проблем.
Модель переноса заряда в РТС
Для расчета ВАХ РТД нами были перепробованы практически все опубликованные
модели [5,6]. Однако ни одна из них не позволяла получить правильное значение
силы тока долины РТД, которая при измерениях всегда оказывалась в несколько
(иногда в десятки и сотни) раз больше, чем теоретическое значение (см.
рис. 1). Этот результат не зависел от топологии и имел место как для
диодов на ![]() -подложке, так и для диодов на полуизолирующей подложке.
-подложке, так и для диодов на полуизолирующей подложке.
Анализ экспериментальных данных позволял утверждать, что неверное теоретическое значение силы тока долины не является следствием неучета в расчетах какого-либо частного явления, а указывает на существенную неполноту описания переноса заряда в рамках традиционно используемых моделей. Как показали расчеты ряда авторов (см., например, [6]), применение более сложных моделей, основанных на формализме матрицы плотности, мало что меняет в лучшую сторону.
Это позволило предположить, что дело не в аппарате, а в неумении адекватно описывать ряд весьма существенных в реальной ситуации факторов.
Одним из таких факторов является случайное взаимодействие, обусловленное рассеянием носителей заряда на фононах, примесях, дефектах решетки и т.д., точные параметры которых неизвестны. Напомним, что в кинетической теории именно такого рода рассеянием обусловлено наличие электрического сопротивления [7].
Была предпринята попытка построить модель переноса заряда, учитывающую как
квантовый характер протекающих процессов, так и наличие случайного
взаимодействия. Полагалось, что действие последнего приводит к процессам
случайного рассеяния частиц, не описываемого детерминированными уравнениями, к
которым относится и уравнение Шредингера с некоторым детерминированным
потенциалом ![]() .
.
Случайное взаимодействие ![]() может быть включено в
потенциал уравнения Шредингера
может быть включено в
потенциал уравнения Шредингера ![]() обычным образом:
обычным образом:
![]() .
.
При этом, однако, неясно, как решать получившееся уравнение?
Мы предположили, что при наличии ![]() каждое квантовое
каждое квантовое ![]() -состояние электронов, определяемое обычной стационарной
теорией как:
-состояние электронов, определяемое обычной стационарной
теорией как:
![]() , (1)
, (1)
здесь ![]() – постоянная Планка,
– постоянная Планка, ![]() – эффективная масса электрона,
– эффективная масса электрона, ![]() и
и ![]() – энергия и волновая
функция электрона,
– энергия и волновая
функция электрона, ![]() – означает
дифференцирование по пространственным координатам и по повторяющимся верхнему и
нижнему индексам происходит суммирование) с детерминированным потенциалом
– означает
дифференцирование по пространственным координатам и по повторяющимся верхнему и
нижнему индексам происходит суммирование) с детерминированным потенциалом ![]() ,
представляет собой как бы самостоятельную фазу некоторого квантового газа [8],
характеризуемую, как это принято в термодинамике, своими температурой
,
представляет собой как бы самостоятельную фазу некоторого квантового газа [8],
характеризуемую, как это принято в термодинамике, своими температурой ![]() и химическим
потенциалом
и химическим
потенциалом ![]() . Действие же
. Действие же
![]() сводится к “перемешиванию” частиц между
фазами. Это “перемешивание”
происходит в соответствии с уравнениями баланса потоков в различных фазах,
которые в простейшем случае, когда все
сводится к “перемешиванию” частиц между
фазами. Это “перемешивание”
происходит в соответствии с уравнениями баланса потоков в различных фазах,
которые в простейшем случае, когда все ![]() равны друг другу и
равны температуре окружающей среды (решетки), выглядят следующим образом:
равны друг другу и
равны температуре окружающей среды (решетки), выглядят следующим образом:
![]() , (2)
, (2)
где ![]() – средняя плотность
электронов в
– средняя плотность
электронов в ![]() -фазе;
-фазе; ![]() – микроскопическая
плотность;
– микроскопическая
плотность; ![]() – средний поток;
– средний поток; ![]() -микроскопический
поток;
-микроскопический
поток; ![]() – оператор градиента;
– оператор градиента; ![]() – некоторая
положительная безразмерная постоянная, характеризующая интенсивность переходов
между состояниями;
– некоторая
положительная безразмерная постоянная, характеризующая интенсивность переходов
между состояниями; ![]() и
и ![]() – выражаются через
квантовомеханическую вероятность переходов между
– выражаются через
квантовомеханическую вероятность переходов между ![]() - и
- и ![]() -состояниями, обусловленными случайным взаимодействием:
-состояниями, обусловленными случайным взаимодействием:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() – некоторый
известный потенциал, отвечающий за тот или иной вид случайного взаимодействия;
– некоторый
известный потенциал, отвечающий за тот или иной вид случайного взаимодействия; ![]() – случайная функция;
– случайная функция; ![]() – функция
распределения, причем:
– функция
распределения, причем:
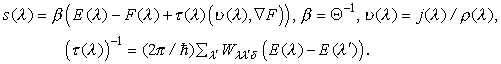
Легко убедиться, что, согласно (2), суммарный поток электронов сохраняется:
![]() ,
,
где ![]() .
.
В случае, когда исследуется перенос заряда в полупроводниковой гетероструктуре, детерминированный потенциал U имеет вид:
![]() ,
,
где ![]() – внешний потенциал,
обусловленный возможным разрывом зон;
– внешний потенциал,
обусловленный возможным разрывом зон; ![]() – заряд электрона;
– заряд электрона; ![]() – самосогласованный
электростатический потенциал, который является решением уравнения Пуассона:
– самосогласованный
электростатический потенциал, который является решением уравнения Пуассона:
![]() , (3)
, (3)
где ![]() – диэлектрическая
проницаемость;
– диэлектрическая
проницаемость; ![]() ;
; ![]() – концентрация
примеси.
– концентрация
примеси.
Граничные условия для уравнений (2), которые по сути являются уравнениями
для химических потенциалов ![]() , даются
равенствами на контактах:
, даются
равенствами на контактах:
![]() ,
,
где ![]() – напряжение на
– напряжение на ![]() -м контакте. Граничные значения потенциала
-м контакте. Граничные значения потенциала ![]() на этих же контактах
находятся из условия электронейтральности:
на этих же контактах
находятся из условия электронейтральности:
![]() .
.
Нормальная производная ![]() полагается равной нулю
на всех границах, переносом заряда через которые можно пренебречь.
полагается равной нулю
на всех границах, переносом заряда через которые можно пренебречь.
Для определения волновых функций ![]() -состояний полагается, что падающие волны в контактных областях
имеют единичную амплитуду, а поток непрерывен. Кроме того, предполагается, что волновые
функции электронов равны нулю на тех границах, перенос заряда через которые
отсутствует.
-состояний полагается, что падающие волны в контактных областях
имеют единичную амплитуду, а поток непрерывен. Кроме того, предполагается, что волновые
функции электронов равны нулю на тех границах, перенос заряда через которые
отсутствует.
Полная плотность тока ![]() вычисляется
суммированием плотностей токов в каждом из электронных состояний:
вычисляется
суммированием плотностей токов в каждом из электронных состояний:
![]() . (4)
. (4)
Система уравнений (1) – (4) и граничные условия полностью определяют задачу о переносе заряда в приборах. Она позволяет вычислять статические ВАХ приборов, а также анализировать неодномерные и нестационарные эффекты в структурах с квантовыми свойствами.
Обратим внимание на самые существенные отличия предлагаемой модели от обычно используемых методов.
Первое – это то, что каждое
электронное состояние рассматривается как самостоятельная термодинамическая
фаза и характеризуется поэтому своим химическим потенциалом ![]() . Кинетика
переходов электронов из одной фазы в другую описывается уравнениями (2),
которые являются релаксационными и имеют в качестве устойчивого аттрактора
состояние равновесия между фазами:
. Кинетика
переходов электронов из одной фазы в другую описывается уравнениями (2),
которые являются релаксационными и имеют в качестве устойчивого аттрактора
состояние равновесия между фазами:
![]() для всех
для всех ![]() и
и ![]() .
.
При этом следует ясно осознавать, что данные переходы, регулируемые разностями химических потенциалов, являются не чем иным, как переходами электронов между различными состояниями, вызванными случайным взаимодействием. Термодинамический язык является только способом численного описания кинетики этих переходов, поскольку динамику со случайным взаимодействием обычно принято сводить к термодинамике [9].
Второе – это наличие “полевого
члена”, пропорционального ![]() , в аргументе функции распределения. Такой вид
, в аргументе функции распределения. Такой вид ![]() не является новостью,
однако с учетом различных
не является новостью,
однако с учетом различных ![]() для разных
для разных ![]() он позволяет связать
воедино квантовое и классическое описания переноса заряда. Действительно,
формула (4) содержит и стандартный дрейфово-диффузионный ток, и “квантовый”
ток, обусловленный несимметрией функций распределения состояний с одинаковыми
энергиями, но разными
он позволяет связать
воедино квантовое и классическое описания переноса заряда. Действительно,
формула (4) содержит и стандартный дрейфово-диффузионный ток, и “квантовый”
ток, обусловленный несимметрией функций распределения состояний с одинаковыми
энергиями, но разными ![]() . Для
иллюстрации разложим
. Для
иллюстрации разложим ![]() по степеням
по степеням ![]() и подставим результат
в (4):
и подставим результат
в (4):
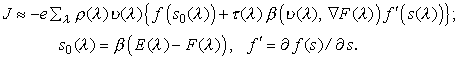
Второй член в выражении для ![]() полностью совпадает с
обычным соотношением для тока в дрейфово-диффузионной модели. Первый член
исчезает в классическом случае, поскольку для каждого
полностью совпадает с
обычным соотношением для тока в дрейфово-диффузионной модели. Первый член
исчезает в классическом случае, поскольку для каждого ![]() в сумме
содержатся состояния с противоположными
в сумме
содержатся состояния с противоположными ![]() и равными
и равными ![]() , а все
, а все ![]() в классической теории
равны между собой по определению.
в классической теории
равны между собой по определению.
В нашей ситуации ![]() могут быть различны
для различных
могут быть различны
для различных ![]() и это приводит к
дополнительному “квантовому” току, который, впрочем, идентичен току,
описываемому известной формулой Цу-Есаки [10].
и это приводит к
дополнительному “квантовому” току, который, впрочем, идентичен току,
описываемому известной формулой Цу-Есаки [10].
В общем виде приведенная здесь модель достаточно сложна для численной
реализации и качественных оценок. Проведенные нами расчеты показали, что в
случае РТС на основе ![]() гетероструктур перенос
заряда может быть достаточно хорошо описан в рамках одномерного приближения в
предположении, что существуют только две электронные фазы: “правых” и “левых”
электронов, т.е. электронов, попадающих в структуру из правой и левой
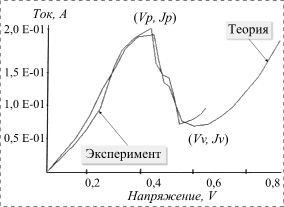
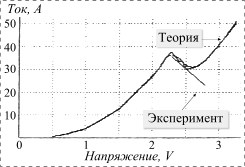
контактных областей соответственно. Результаты некоторых расчетов показаны на
рис. 2 и рис 3.
гетероструктур перенос
заряда может быть достаточно хорошо описан в рамках одномерного приближения в
предположении, что существуют только две электронные фазы: “правых” и “левых”
электронов, т.е. электронов, попадающих в структуру из правой и левой
контактных областей соответственно. Результаты некоторых расчетов показаны на
рис. 2 и рис 3.
|
|
|
|
Рис. 2. Типичные ВАХ РТД на хорошо проводящей n+-подложке |
Рис. 3. Типичные ВАХ РТД на полуизолируюшей подложке |
Чтобы понять, какие факторы позволили столь хорошо описать экспериментальную ситуацию, выпишем уравнение для тока, получающееся из (4) после суммирования по импульсам, перпендикулярным направлению переноса:
![]() , (5)
, (5)
где ![]() , а интеграл
по энергиям берется от максимального из значений потенциала
, а интеграл
по энергиям берется от максимального из значений потенциала ![]() на левом или правом
контактах и до бесконечности.
на левом или правом
контактах и до бесконечности.
Если приблизительно считать, что ![]() и
и ![]() , то из (5) получим формулу Цу-Есаки [10]. Однако, в отличие
от нее, выражение (5) является локальным, явно содержит полевой вклад и, кроме
того, неявно содержит релаксационный ток, обусловленный неравновесностью между
“левыми” и “правыми” электронами.
, то из (5) получим формулу Цу-Есаки [10]. Однако, в отличие
от нее, выражение (5) является локальным, явно содержит полевой вклад и, кроме
того, неявно содержит релаксационный ток, обусловленный неравновесностью между
“левыми” и “правыми” электронами.
До тех пор, пока резонансный уровень в РТС “работает”, полевой член и вклад релаксации оказываются несущественными. Но как только приложенное напряжение искажает потенциальный рельеф настолько, что резонанс исчезает, важнейшими становятся именно эти вклады.
При реальных высотах барьеров (порядка 1 эВ) наблюдаемые высокие токи долины невозможно объяснить надбарьерной проводимостью. Но, если принять во внимание, что полевые вклады в (5) и в числителе, и в знаменателе логарифма направлены на повышение силы тока, то экспериментальные значения силы токов долины становятся легко объяснимыми.
Исчезновение резонансного уровня приводит к резкому
увеличению градиентов ![]() и их разности
и их разности ![]() в области барьеров.
Большие градиенты химических потенциалов приводят к возникновению
дополнительных “квазидрейфово-диффузионных” токов.
в области барьеров.
Большие градиенты химических потенциалов приводят к возникновению
дополнительных “квазидрейфово-диффузионных” токов.
Дополнительно, из-за резкого возрастания разности ![]() – существенным
становится релаксационный ток, обусловленный переходами “правых” электронов в
“левые”, что также ведет к существенному увеличению силы тока в области
падающего участка ВАХ РТС. Именно этим процессом и обусловлено, на наш взгляд,
образование часто наблюдаемой “полочки” на этом участке ВАХ (см. рис. 2 и рис. 3).
– существенным
становится релаксационный ток, обусловленный переходами “правых” электронов в
“левые”, что также ведет к существенному увеличению силы тока в области
падающего участка ВАХ РТС. Именно этим процессом и обусловлено, на наш взгляд,
образование часто наблюдаемой “полочки” на этом участке ВАХ (см. рис. 2 и рис. 3).
Взаимодействие классических и квантовых областей РТД
Одним из первых, кто обратил внимание на принципиальную важность учета взаимодействия классических и квантовых областей приборов, был О.Т.Гаврилов. Им же были выполнены и первые исследования этого взаимодействия для РТД [11-13].
Неоспоримым является то, что какими бы квантовыми явлениями не определялись характеристики микроструктур, в конечном счете, в качестве среды, через которую эти структуры взаимодействуют с другими структурами, устройствами и пр., выступают макроскопические области. Во многих случаях эти макроскопические области играют роль не просто “приемщиков” и “передатчиков” сигналов, но и существенно влияют на характеристики самих микроструктур, например, путем искажения потенциального рельефа.
Это влияние может иметь “катастрофические” последствия, т.е. приводить к таким искажениям выходных характеристик, которые делают приборы на основе микроструктур неработоспособными. Кроме того, с этим влиянием могут быть связаны новые эффекты, пригодные для использования в электронных устройствах [12].
Предложенная выше модель позволяет описывать квантовые и классические области приборов в рамках единого формализма. Однако реализация такого описания требует значительных затрат программистского труда и существенных вычислительных ресурсов. Работы в этом направлении были начаты в 90-е годы, но не закончены. Единое описание было реализовано только в рамках одномерного приближения, чего совершенно недостаточно для решения прикладных задач.
По этой причине О.Т.Гавриловым был параллельно развит “гибридный” подход, в рамках которого квантовые и частично классические области РТС описывались на основе приведенной выше модели в одномерном приближении, а подложка описывалась исключительно классически на основе уравнений:
![]() ,
, ![]() (6)
(6)
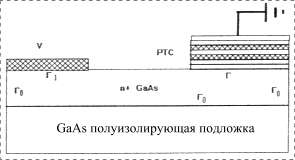
и граничных условий (рис. 4):
![]() ,
, ![]() ,
, ![]() .
(7)
.
(7)
|
|
|
Рис. 4. РТД на полуизолирующей подложке |
Здесь ![]() – плотность тока в
подложке;
– плотность тока в
подложке; ![]() – проводимость
подложки;
– проводимость
подложки; ![]() – внешняя нормаль к
границе;
– внешняя нормаль к
границе; ![]() – плотность тока РТС, вычисленная на
основе одномерной модели и взятая на некоторой фиктивной границе
– плотность тока РТС, вычисленная на
основе одномерной модели и взятая на некоторой фиктивной границе ![]() между РТС и подложкой.
Существенно, чтобы на этой границе электроны уже можно было бы считать
равновесными (в смысле равенства их химических потенциалов). Заметим, что уравнения
(6) учитывают и дрейфовую и диффузионную составляющие плотности тока.
между РТС и подложкой.
Существенно, чтобы на этой границе электроны уже можно было бы считать
равновесными (в смысле равенства их химических потенциалов). Заметим, что уравнения
(6) учитывают и дрейфовую и диффузионную составляющие плотности тока.
Решение краевой задачи (6), (7) существенно улучшает соответствие между теорией и экспериментом. Это наглядно продемонстрировано на рис. 5, где изображены экспериментальная и расчетные ВАХ РТД до учета влияния подложки и после этого учета.
Следует отметить, что, как показал анализ [11-13], взаимодействие РТС с подложкой, отнюдь, не сводится к тривиальному эффекту нагрузочного сопротивления. Необычный вид второго из граничных условий (7) приводит к двум интересным следствиям:
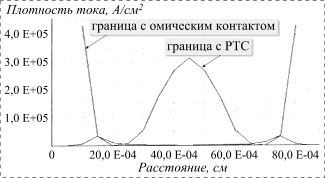
· распределение нормальной составляющей плотности тока на границе Г имеет нестандартный для решений уравнения Лапласа вид (рис. 6);
· при определенных соотношениях между проводимостью РТС на участках ВАХ с отрицательной дифференциальной проводимостью, проводимостью подложки и геометрическими размерами структуры задача (6), (7) может иметь неединственное решение [11] и даже бесконечный спектр собственных решений [12].
|
|
|
|
Рис. 5. Теоретические и экспериментальная ВАХ РТД на полуизолирующей подложке |
Рис. 6. Распределение нормальной составляющей плотности тока вдоль границы между РТС и n+-подложкой |
Первая из отмеченных особенностей означает, что далеко не вся площадь “контакта” между РТС и подложкой “работает” в одинаковом режиме. Какая-то часть соответствует участкам ВАХ РТС с отрицательной проводимостью, другая – участкам ВАХ с положительной проводимостью. Все это приводит к нетривиальной зависимости ВАХ РТД от проводимости подложки, ее топологии и площадей контактных областей. Этот вывод был подтвержден и экспериментальными исследованиями [13].
Вторая особенность делает возможным использование подложки РТД для весьма необычных приборных решений. В частности, она может выступать в качестве резонатора электромагнитных колебаний СВЧ и КВЧ диапазонов [12].
Построенная модель позволяет оценивать влияние подложки на характеристики приборов и конструировать РТД с заранее заданными свойствами.
![]()
В статье приведены некоторые результаты
работ по моделированию характеристик РТС и РТД, проводившихся в период создания этих структур и приборов в
СССР и России.
Показано, какие факторы существенным образом влияют на наблюдаемые в эксперименте характеристики приборов. Продемонстрировано, что построенные модели позволяют описывать статические характеристики РТД адекватно эксперименту.
Список литературы
1. Nanotechnology Research Directions
// IWGN Workshop Report (January, 1999) / M.С.Roco, R.S.Williams and P.Alivisatos, Kluwer
Academic Publishers.
2. Obukhov I.A. The new model of charge transport in quantum devices // Proceeding of NANO-II. Part C. Moscow, 1993. P. 889-896.
3. Obukhov I.A. Resonant-tunneling diode theory and modeling // Proceeding of NANOMEETING-95. Physics, Chemistry and Application of Nanostructures. Minsk, 1995. P. 271-272.
4. Obukhov I.A. The local models of charge transport // Proceeding of NANOMEETING-95, Physics, Chemistry and Application of Nanostructiires Minsk, 1995. P. 273-276.
5. Frontiers in Nanoscale Science of
Micron // Submicron Devices, NATO ASI Series. E-328 / Edited by Antti-Pekka
Jauho and Eugenia V.Buzaneva. Kluwer Academic Publishers.
6. Kluksdahl N.C., Kriman A.M. et al Phys. Rev. В. V. 39. 1989. P. 772.
7. Гринвуд Д. Кинетическое уравнение в теории электропроводности металлов // Вопросы квантовой теории необратимых процессов / Под ред. В.Л. Бонч-Бруевича M., 1961. С. 201-224.
8. Петров Н., Бранков Й. Современные проблемы термодинамики М.: Мир, 1986. 286 с.
9. Репке Г. Неравновесная статистическая механика М.: Мир, 1990. 320 с.
10. Tsu R., Esaki L. Appl. Phys. Lett. V. 22. 1973. P. 562.
11. Gavrilov О.Т., Obukhov I.A., Dianov S.A. The classical regions influence on characteristics of Resonant-Tunneling Diode // Proceeding of NANO-II, Part. С. Moscow, 1993. P. 860-870.
12. Gavrilov О.Т., Kvyatkevich I.I., Obukhov I.A., Matveev Yu.A. Interaction of a resonant tunnel diode with the substrate through a distributed interface // Tech. Phys. Lett. V. 22. 1996. P. 311-312.
13. Гаврилов О.Т., Квятксвич И.И., Обухов И.А. Влияние классических областей на характеристики резонансно-туннельного диода // Материалы 7-й Крымской Микроволновой Конференции Севастополь, 1997. С. 401-403.
| Наверх |