Л.В. Беликов, канд. техн. наук, Институт биохимической физики РАН
ПРОЕКТИРОВАНИЕ ТОПОЛОГИИ
ТЕНЗОРЕЗИСТОРНОГО МОСТА УИТСТОНА, РАСПОЛОЖЕННОГО НА МОНОКРИСТАЛЛИЧЕСКОЙ
КРЕМНИЕВОЙ МЕМБРАНЕ, ОРИЕНТИРОВАННОЙ ПО (111)
![]()
|
Дан метод определения правой и левой поверхностей и нижней границ
области, занимаемой тензорезисторами p- и n-типов проводимости, расположенных на монокристаллической кремниевой
мембране, ориентированной по кристаллографической плоскости (111). Показано
формирование полных мостов Уитстона |
Имеем монокристаллическую кремниевую (МК) мембрану
толщиной ![]() , которая защемлена по контуру радиуса
, которая защемлена по контуру радиуса ![]() и нагружена
распределенным давлением интенсивности
и нагружена
распределенным давлением интенсивности ![]() . Планарная сторона этой мембраны ориентирована по
кристаллографической плоскости (111). Под проектированием топологии полного
активного моста Уитстона из тензорезисторов
. Планарная сторона этой мембраны ориентирована по
кристаллографической плоскости (111). Под проектированием топологии полного
активного моста Уитстона из тензорезисторов ![]() - или
- или ![]() -типов проводимости будем понимать определение радиуса
-типов проводимости будем понимать определение радиуса ![]() и толщины
и толщины ![]() мембраны или их
отношения, а также положения правой
мембраны или их
отношения, а также положения правой ![]() и левой
и левой ![]() , верхней
, верхней ![]() и нижней
и нижней ![]() границ области,
занимаемой каждым из четырех тензорезисторов на мембране относительно ее центра
таким образом, чтобы относительное изменение сопротивления
границ области,
занимаемой каждым из четырех тензорезисторов на мембране относительно ее центра
таким образом, чтобы относительное изменение сопротивления ![]() было максимальным. Тензорезисторы,
расположенные в смежных плечах моста, должны при этом иметь равные по значению,
но противоположные по знаку изменения относительного сопротивления
было максимальным. Тензорезисторы,
расположенные в смежных плечах моста, должны при этом иметь равные по значению,
но противоположные по знаку изменения относительного сопротивления ![]() . Начало декартовых координат совпадает с центром мембраны.
. Начало декартовых координат совпадает с центром мембраны.
Известно [1, с.235], что наиболее опасными точками на
мембране являются точки у её заделки. Если верхний предел измеряемого давления ![]() известен, то из [1]
имеем:
известен, то из [1]
имеем:
![]() экв
экв![]() ,
,
где ![]() – коэффициент
Пуассона.
– коэффициент
Пуассона.
С учетом того, что в кристаллографической плоскости (111) коэффициент Пуассона МК равен 0,262, имеем окончательно:
![]() экв
экв![]() ,
,
где [![]() ] – допускаемое напряжение.
] – допускаемое напряжение.
Поскольку в настоящее время прочностные характеристики МК достоверно
неизвестны, то на основании данных [11] о переделе прочности химически
полированного МК, в первом приближении [![]() ] можно принять равным
] можно принять равным ![]() Па, что подтверждается
данными, приведенными в [16]. Таким образом, удается определить отношение (
Па, что подтверждается
данными, приведенными в [16]. Таким образом, удается определить отношение (![]() ).
).
Номинальное сопротивление тензорезистора без учета влияния контактных площадок и легирования под окисной маской определяется отношением:
![]() (число “квадратов”)
(число “квадратов”)
и уровнем легирования ![]() (“сопротивление слоя”)
[4,14,18].
(“сопротивление слоя”)
[4,14,18].
В [5,6] описаны попытки решения этой задачи. В первом
случае [5] тензорезисторы ![]() -типа проводимости имели П-образную форму, их продольные оси
были параллельны кристаллографическим направлениям [110], причем центр тяжести
одного тензорезистора расположен на расстоянии
-типа проводимости имели П-образную форму, их продольные оси
были параллельны кристаллографическим направлениям [110], причем центр тяжести
одного тензорезистора расположен на расстоянии ![]() от центра мембраны, а
центр тяжести тензорезистора, расположенного в смежном плече моста – на
расстоянии
от центра мембраны, а
центр тяжести тензорезистора, расположенного в смежном плече моста – на
расстоянии ![]() . Каких-либо обоснований этому типу топологии дано не было.
. Каких-либо обоснований этому типу топологии дано не было.
Во втором случае [6] для тензорезисторов ![]() -типа проводимости были приведены выражения чувствительности
-типа проводимости были приведены выражения чувствительности ![]() тензорезистора
расположенного в центральной части мембраны, в виде:
тензорезистора
расположенного в центральной части мембраны, в виде:
![]() ,
(1а)
,
(1а)
а для тензорезистора, расположенного на периферийной части мембраны, в виде:
![]() ,
(1б)
,
(1б)
причем число диффузионных областей ![]() , из которых набирается тензорезистор, для тензорезистора,
расположенного в центре мембраны, равно:
, из которых набирается тензорезистор, для тензорезистора,
расположенного в центре мембраны, равно:
![]() , (1в)
, (1в)
а для тензорезистора, расположенного на периферии мембраны, оно равно:
![]() . (1г)
. (1г)
В этих уравнениях ![]() – общая длина
тензорезистора;
– общая длина
тензорезистора; ![]() – шаг тензорезистора;
– шаг тензорезистора; ![]() – угол сектора мембраны,
в котором располагается тензорезистор.
– угол сектора мембраны,
в котором располагается тензорезистор.
Следует особо отметить, что продольная ось
тензорезистора, расположенного в центральной части мембраны, имеет вид дуги
окружности, а продольная ось тензорезистора, размещенного на периферийной части
мембраны, имеет вид отрезка прямой. Получить номинальное значение сопротивления
таких тензорезисторов с минимальным разбросом не представляется возможным. Не
определено, почему величина ![]() должна отличаться от 2
(а именно столько должно быть активных тензорезисторов), почему число
должна отличаться от 2
(а именно столько должно быть активных тензорезисторов), почему число ![]() должно быть разным для
центрального и периферийного тензорезисторов.
должно быть разным для
центрального и периферийного тензорезисторов.
В [8] относительное изменение сопротивления ![]() - тензорезистора
- тензорезистора ![]() -типа проводимости, расположенного на такой мембране, дано в
виде:
-типа проводимости, расположенного на такой мембране, дано в
виде:
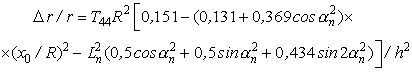 , (2)
, (2)
где ![]() – фундаментальный
сдвиговый тензорезистивный коэффициент первого рода;
– фундаментальный
сдвиговый тензорезистивный коэффициент первого рода; ![]() – угол между осью “
– угол между осью “![]() ” и продольной осью тензорезистора;
” и продольной осью тензорезистора; ![]() – длина
– длина ![]() -го участка тензорезистора.
-го участка тензорезистора.
Следует отметить, что в расчетах, проведенных в этой
работе, продольный ![]() и поперечный
и поперечный ![]() фундаментальные
тензорезистивные коэффициенты приняты равными нулю, что, на наш взгляд, вносит
дополнительные погрешности при проектировании датчика давления. Следует
признать, что спроектировать топологию по уравнению (2) представляется
достаточно сложным делом. И в работе [10], и последующей работе [9]
предпринимались попытки решить задачу в самом общем виде, пренебрегая
продольным
фундаментальные
тензорезистивные коэффициенты приняты равными нулю, что, на наш взгляд, вносит
дополнительные погрешности при проектировании датчика давления. Следует
признать, что спроектировать топологию по уравнению (2) представляется
достаточно сложным делом. И в работе [10], и последующей работе [9]
предпринимались попытки решить задачу в самом общем виде, пренебрегая
продольным ![]() и поперечным
и поперечным ![]() тензорезистивными
коэффициентами для тензорезисторов
тензорезистивными
коэффициентами для тензорезисторов ![]() -типа, а также сдвиговым
-типа, а также сдвиговым ![]() тензорезистивным
коэффициентом – для тензорезисторов
тензорезистивным
коэффициентом – для тензорезисторов ![]() -типа соответственно, что представляется довольно
сомнительным.
-типа соответственно, что представляется довольно
сомнительным.
В [20] относительное изменение сопротивления ![]() тензорезистора
тензорезистора ![]() -типа проводимости, расположенного на такой мембране,
записано в виде:
-типа проводимости, расположенного на такой мембране,
записано в виде:
![]() ,
(3)
,
(3)
где ![]() – текущая координата
тензорезистора;
– текущая координата
тензорезистора; ![]() – безразмерный коэффициент,
характеризующий несовершенство защемления мембраны.
– безразмерный коэффициент,
характеризующий несовершенство защемления мембраны.
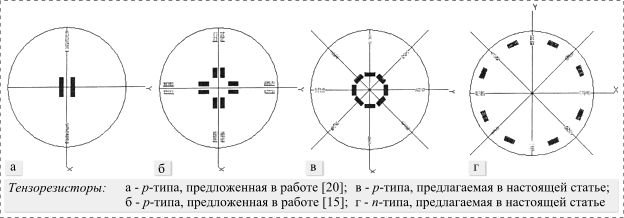
Следует отметить, что в полученных уравнениях безразмерная величина (левая часть уравнения) имеет размерность в паскалях (правая часть уравнения), а потому к выводам этой работы надо относиться с осторожностью. Предложенная в [20] топология имеет ось симметрии 2-го порядка (рис. 1,а) (сплошная штриховка тензорезисторов обозначает отрицательное приращение сопротивления, а слабая штриховка – положительное приращение сопротивления).
В работах [11,17,21,24,25] рассмотрены вопросы проектирования датчиков давления с фольговыми тензорезисторами и приведены топологии полных активных мостов Уитстона. В силу изотропии электрофизических свойств МК в кристаллографической плоскости (111) [3,13] должна соблюдаться полная аналогия – продольная ось тензорезисторов должна совпадать в центральной части мембраны с окружным направлением мембраны, а у края мембраны – с радиальным направлением мембраны. Так, собственно говоря, и показано в работе [6].
В [15] на основании работы [8] дана топология такой мембраны. Предложенная в этой работе топология имеет ось симметрии 4-го порядка (рис. 1,б).
Поскольку проектирование топологии по формулам,
имеющимся в [6,10,20], представляется достаточно сложным и не отвечает на главный
вопрос о положении границ ![]() ,
, ![]() ,
, ![]() ,
, ![]() области, занимаемой
тензорезистором, продолжим развивать метод проектирования, предложенный нами
ранее [3,13]. В расчетах будем принимать, что фундаментальные коэффициенты
податливости МК [7,10,22] равны соответственно:
области, занимаемой
тензорезистором, продолжим развивать метод проектирования, предложенный нами
ранее [3,13]. В расчетах будем принимать, что фундаментальные коэффициенты
податливости МК [7,10,22] равны соответственно:
![]() Па
Па![]() ;
(4а)
;
(4а)
![]() Па
Па![]() ;
(4б)
;
(4б)
![]() Па
Па![]() .
(4в)
.
(4в)
Значения коэффициентов приведены по американским данным, в которых отсутствуют сведения о типе легирующей примеси и ее концентрации. Но в качестве предварительных данных ими, безусловно, можно пользоваться.
Фундаментальные продольный ![]() , поперечный
, поперечный ![]() и сдвиговый первого
рода
и сдвиговый первого
рода ![]() тензорезистивные
коэффициенты для МК
тензорезистивные
коэффициенты для МК ![]() -типа проводимости равны соответственно [22]:
-типа проводимости равны соответственно [22]:
![]() Па
Па![]() ;
(5а)
;
(5а)
![]() Па
Па![]() ;
(5б)
;
(5б)
![]() Па
Па![]() .
(5в)
.
(5в)
Те же коэффициенты для МК ![]() -типа проводимости равны [22]:
-типа проводимости равны [22]:
![]() Па
Па![]() ;
(6а)
;
(6а)
![]() Па
Па![]() ;
(6б)
;
(6б)
![]() Па
Па![]() .
(6в)
.
(6в)
Эти данные для объемно-легированного МК можно принять
в качестве предварительных, поскольку достоверных данных для диффузионных и
ионно-легированных слоев на кремнии, если не считать данных [26], нет и в
настоящее время. В [26] приведены значения фундаментальных тензорезистивных
коэффициентов для диффузионных слоев ![]() -типа
-типа
![]() Па
Па![]() ;
;
![]() Па
Па![]() ;
;
![]() Па
Па![]() ,
,
что по мнению автора соответствует поверхностной
концентрации легирующей примеси примерно ![]() см3.
см3.
Следует заметить, что достаточно подробный справочник по свойствам полупроводниковых материалов [2] подобных сведений также не приводит.
Относительное изменение сопротивления ![]() “точечного”
тензорезистора, находящегося на круглой защепленной по контуру МК мембране с
ориентацией по кристаллографической плоскости (111), будет равно [27]:
“точечного”
тензорезистора, находящегося на круглой защепленной по контуру МК мембране с
ориентацией по кристаллографической плоскости (111), будет равно [27]:
![]() , (7)
, (7)
где ![]() и
и ![]() - главные напряжения по осям
- главные напряжения по осям ![]() и
и ![]() в рассматриваемой
точке мембраны.
в рассматриваемой
точке мембраны.
По [23] эти напряжения равны соответственно:
![]() ; (8а)
; (8а)
![]() , (8б)
, (8б)
где ![]() – коэффициент Пуассона
материала мембраны.
– коэффициент Пуассона
материала мембраны.
Ранее нами [3,13] были получены для
кристаллографической плоскости (111) выражения для продольного ![]() и поперечного
и поперечного ![]() тензорезистивных
коэффициентов и коэффициента Пуассона в виде:
тензорезистивных
коэффициентов и коэффициента Пуассона в виде:
![]() ;
(9а)
;
(9а)
![]() ; (9б)
; (9б)
![]() . (9в)
. (9в)
Тогда на основании уравнений относительное изменение
сопротивления ![]() “точечного” тензорезистора
“точечного” тензорезистора
![]() -типа проводимости, когда направление между электрическими
контактами совпадает с радиальным направлением мембраны, будет:
-типа проводимости, когда направление между электрическими
контактами совпадает с радиальным направлением мембраны, будет:
![]() рад, р
рад, р ![]() Па
Па![]()
![]() , (10а)
, (10а)
а когда направление между электрическими контактами совпадает с окружным направлением мембраны, будет соответственно:
![]() окр, р
окр, р ![]() Па
Па![]()
![]() . (10б)
. (10б)
Для “точечного” тензорезистора ![]() -типа проводимости, когда направление между электрическими
контактами совпадает с радиальным направлением мембраны, имеем
-типа проводимости, когда направление между электрическими
контактами совпадает с радиальным направлением мембраны, имеем
![]() рад, п
рад, п![]() Па
Па![]()
![]() , (10в)
, (10в)
когда направление между электрическими контактами совпадает с окружным направлением мембраны, имеем соответственно:
![]() окр, п
окр, п![]() Па
Па![]()
![]() . (10г)
. (10г)
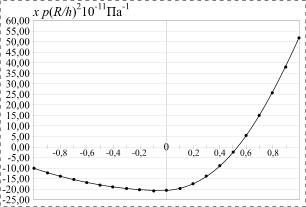
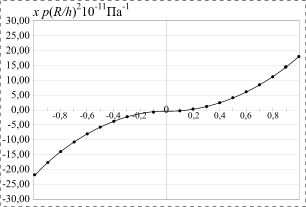
На рис. 2 и 3 приведены эпюры относительного
изменения сопротивления ![]() “точечных” радиальных
и окружных тензорезисторов обоих типов проводимости, полученные в результате
расчета по уравнениям (10а – 10г).
“точечных” радиальных
и окружных тензорезисторов обоих типов проводимости, полученные в результате
расчета по уравнениям (10а – 10г).
|
|
|
|
Рис. 2. Относительное изменение сопротивления “радиальных” (справа) и “окружных” (слева) точечных тензорезисторов p-типа |
Рис. 3. Относительное изменение сопротивления “радиальных” (справа) и “окружных” (слева) точечных тензорезисторов n-типа |
Из этих рисунков видно, что продольные оси
тензорезисторов ![]() -типа проводимости должны располагаться параллельно
координатным осям в центре мембраны. Смежные плечи моста Уитстона из тензорезисторов
-типа проводимости должны располагаться параллельно
координатным осям в центре мембраны. Смежные плечи моста Уитстона из тензорезисторов
![]() -типа проводимости должны быть расположены в радиальном
направлении на расстоянии примерно
-типа проводимости должны быть расположены в радиальном
направлении на расстоянии примерно ![]() .
.
Нам представляется, что топология такой мембраны с
мостом Уитстона из тензорезисторов ![]() -типа проводимости должна иметь ось симметрии 8-го или даже
16-го порядка. Топология такой мембраны с мостом Уитстона из тензорезисторов
-типа проводимости должна иметь ось симметрии 8-го или даже
16-го порядка. Топология такой мембраны с мостом Уитстона из тензорезисторов ![]() -типа проводимости также должна иметь ось симметрии 8-го,
16-го и даже более высокого порядка. Это позволит иметь более равномерный
нагрев ее протекающим током, что особенно важно для мембран, толщина которых не
превышает 30 мкм.
-типа проводимости также должна иметь ось симметрии 8-го,
16-го и даже более высокого порядка. Это позволит иметь более равномерный
нагрев ее протекающим током, что особенно важно для мембран, толщина которых не
превышает 30 мкм.
Уточненный расчет положения границ тензорезисторов получается в результате интегрирования тензоэффекта по площади, занимаемой тензорезисторами, и последующем усреднении результата, т.е.:
![]() . (11)
. (11)
Тогда уравнения примут окончательный вид:
![]() рад, р
рад, р ![]()
![]() Па
Па![]()
![]() ; (12а)
; (12а)
![]() окр, р =
окр, р =
![]() Па
Па![]()
![]() ; (12б)
; (12б)
![]() рад, n
рад, n ![]()
![]() Па
Па![]()
![]() ; (12в)
; (12в)
![]() окр, n =
окр, n =
![]() Па
Па![]()
![]() . (12г)
. (12г)
Этапы проектирования топологии таковы:
·
по верхнему пределу измеряемого давления ![]() определяем отношение (
определяем отношение (![]() );
);
· выбираем тип ионного легирования (или диффузии) – “базовое” или “эмиттерное”;
· выбираем форму тензорезисторов и их ширину;
· определяем число “квадратов”, т.е. номинальное сопротивление;
· выбираем тип симметрии топологии, которая, на наш взгляд, должна иметь ось симметрии не ниже 4-го порядка;
· вычерчиваем положение тензорезисторов в центральной части мембраны;
·
по уравнению (12а) находим относительное
изменение сопротивления ![]() тензорезистора
тензорезистора ![]() -типа проводимости, причем “число квадратов” в нем должно
быть равно половине номинального значения “числа квадратов” и левая граница
-типа проводимости, причем “число квадратов” в нем должно
быть равно половине номинального значения “числа квадратов” и левая граница ![]() должна принимать значение,
равное нулю, в силу того, что при расчете начало координат совпадает с центром
мембраны;
должна принимать значение,
равное нулю, в силу того, что при расчете начало координат совпадает с центром
мембраны;
· зная примерное положение центра тензорезистора, находящегося в смежном плече моста, с помощью итерационных вычислений определяем его положение по уравнению (12а).
![]()
Таким образом, полученные в настоящей работе уравнения
(10а, 10б) для тензорезисторов ![]() -типа и уравнения (10в, 10г) для тензорезисторов
-типа и уравнения (10в, 10г) для тензорезисторов ![]() -типа позволяют определить правую и левую верхнюю и нижнюю
границы области, занимаемой “окружными” и “радиальными” тензорезисторами, в
зависимости от верхнего предела измерений и параметров
-типа позволяют определить правую и левую верхнюю и нижнюю
границы области, занимаемой “окружными” и “радиальными” тензорезисторами, в
зависимости от верхнего предела измерений и параметров ![]() и
и ![]() МК-мембраны
МК-мембраны
Список литературы
1. Андреева Л.Е. Упругие элементы приборов М.: Машгиз, 1962.
2. Баранский П.И., Клочков В.П., Потыкевич И.В. Полупроводниковая электроника. Свойства материалов (Справочник), Киев: Наукова думка, 1975. 704 с.
3. Беликов Л.В., Берников В.Б., Евдокимов В.И., Заседателев С.М., Киселевский С.Л., Сгибов А.П. О проектировании датчиков давления с “интегральными” тензопреобразователями. М.: ЦНИИТЭИ приборостроения, 1971. 20 с.
4. Березин А.С., Мочалкииа О.Р. Технология и конструирование интегральных микросхем. М.: Радио и связь, 1983. 232 с.
5. Ваганов В.И., Пономарев К.М. Кремниевый манометрический элемент для интегральных преобразователей малых давлений, Материалы XXII научно-технической конференции “Физическая электроника”. Вып. 1. Каунас: Изд. Каунасского политех. Института. 1972. С. 125-130.
6. Ваганов В.И., Пономарев К.М. Исследование свойств диффузионных тензорезисторов преобразователей давления с кремниевыми мембранами. // Измерительная техника. 1973. № 7. С. 35-36.
7. Вустер У. Применение тензоров и теории групп для описания физических свойств кристаллов. / Пер. с англ. М.: Мир, 1977. 383 с.
8. Гридчин В.А. Расчет интегральной тензочувствительной мостовой схемы на круглой мембране. // Физика и техника полупроводников. Новосибирск: НЭТИ. 1974. С. 120-133.
9. Гридчин В.А. Физические вопросы проектирования кремниевых интегральных тензопреобразователей. // Физические основы полупроводниковой тензометрии. Новосибирск: НЭТИ. 1981. С. 48-80.
10. Гридчнн В.А., Алексеев В.В., Осинцова Л.А., Шадрин В.С. Кремниевый упругий элемент мембранного типа с диффузионными тензорезисторами. // Физика и техника полупроводников. Новосибирск: НЭТИ. 1970. С. 3-8.
11. Джексон П. Датчики сопротивления из фольги. // Прикладная механика и машиностроение. 1954. № 5(17). С. 88-103.
12. Еланская Л.Г., Фомина В.Г. Прочность некоторых полупроводниковых монокристаллов при комнатной температуре. // Труды ГИРЕДМЕТ. Вып. 66. 1974. С. 19-25.
13. Заседателев С.М., Беликов Л.В., Берников В.Б., Евдокимов В.И., Киселевский С.Л., Сгибов А.П. О проектировании датчиков давления с интегральными тензопреобразователями. // Приборы и системы управления. 1971. № 11. С. 45-48.
14. Интегральные схемы. Принцип конструирования и производства. / Пер с англ. М.: Советское радио, 1968. 264 с. (с. 178-184)
15. Кальпус В.Ю., Куракова Л.М. Влияние технологических факторов на тензочувствительность элементов мембранного типа. // Физика и техника полупроводников. Новосибирск: НЭТИ, 1976. С. 106-113.
16. Концевой Ю.А., Литвинов Ю.М., Фаттахов Э.А. Пластичность и прочность полупроводниковых материалов и структур. М.: Радио и связь, 1982. 240 с.
17. Майзель М.Б. К вопросу чувствительности диафрагменного манометра с фольговыми тензодатчиками. // Приборостроение. 1960. № 9. С. 5-7.
18. Мэдленд Г.Р., Дикен Г.К., Ричардсон Р.Д., Притчард Р.Л., Боуер Ф.Г., Крет Д.Б. Интегральные схемы. Основы проектирования и технологии. / Пер. с англ. М.: Советское радио, 1970. 952 с.
19. Най Дж. Физические свойства кристаллов и их описание при помощи тензоров и матриц. / Пер. с англ. М.: Мир 1967. 386 с.
20. Пивоненков Б.И., Стучебников В.М. Проектирование полупроводниковых интегральных тензочувствительных структур. // Приборы и системы управления. 1976. № 1. С. 20-21.
21. Синев А.В., Этингоф М.И. О выборе формы датчиков давления с фольговыми тензодатчиками. // Приборостроение. 1966. № 9. С. 6-8.
22. Терстон Р. Применение полупроводниковых преобразователей для измерения деформаций, ускорений и смещений. // Физическая акустика. Под ред. У. Мэзона. Т. 1. Часть “Б”. / Пер. с англ. М.: Мир, 1967. С. 187-209.
23. Тимошенко С.П., Лессельс Дж. Прикладная теория упругости. Изд. 3-е, стереотипное / Пер. с англ. М. – Л.: ГНТИ, 1931. 392 с.
24. Этингоф М.И., Синев А.В. Особенности расчета электротензометрических датчиков давления. // Труды ЦНИИТМаш. Вып. 61. 1966. С. 105-110.
25. Этингоф М.И., Синев А.В., Фролов К.В. К расчету мембранного тензометрического датчика давления повышенной чувствительности. // Труды ЦНИИТМаш. Вып. 62. 1966. С. 114-123.
26. Fulkerson D.Е. A Silicon Integrated Circuit Force Sensor. // IEEE Trans. Electron Devices. 1969. V. ED-16. № 10. P. 867-870.
27. Tufte O.N., Chapman P.W.,
Long D. Silicon Diffused Element Piezoresistive Diaphragms. //
J. Appl. Phys. 1962. V. 33. № 11. P. 3322-3327.
| Наверх |