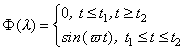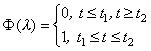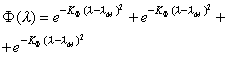УДК 681.782.473:517

С.А. Матюнин, канд. техн. наук, доц., Самарский государственный аэрокосмический университет, Г.И. Леонович, д-р техн. наук, доц., Секция прикладных проблем при Президиуме РАН

ИСПОЛЬЗОВАНИЕ ФУНКЦИЙ ГАУССА ДЛЯ АППРОКСИМАЦИИ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОМПОНЕНТНЫХ ОПТРОННЫХ СТРУКТУР

Рассмотрена аппроксимация характеристик оптоэлектронных элементов рядом функций Гаусса, позволяющая существенно сократить число членов ряда и повысить точность аппроксимации.

При решении задач проектирования и повышения точности оптоэлектронных измерительных преобразователей и других оптоэлектронных приборов часто возникает проблема адекватного математического описания передаточных характеристик информационных каналов [1-3]. Это связано с большим числом компонентов в составе оптронных структур (источники излучения, фотоприемники, оптические фильтры и т.д.), пространственные, спектральные, временные и температурные характеристики которых имеют сложную форму. При переходе от теоретического описания к практическим расчетам удачный выбор аппроксимирующей функции, обеспечивающей заданную точность аппроксимации при малом числе членов разложения, во многом определяет простоту и удобство дальнейшего анализа и синтеза преобразователей.

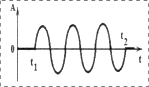
Применение степенных рядов и конформных отображений приводит, как правило, к значительному числу членов ряда [4,5]. Например, аппроксимация цуга (отрезка) синусоидальной волны тригонометрическим рядом Фурье дает плохо сходящийся бесконечный ряд. Задача усложняется в случае теоретического анализа и оптимизации отдельных ключевых характеристик аппаратуры. Такая ситуация, в частности, имеет место при аппроксимации характеристик оптоэлектронных элементов многокомпонентных оптронных структур (МОС) спектрального взаимодействия, когда возникает необходимость с достаточно высокой точностью знать аналитическую зависимость спектральных и пространственных характеристик оптоэлектронных элементов (ОЭЭ) от многочисленных факторов.

Накопленный опыт теоретических и экспериментальных исследований позволяет авторам сделать вывод, что в качестве альтернативного метода аппроксимации передаточной функции МОС для обеспечения точности и быстрой сходимости ряда может использоваться ряд гауссиан [3,4]. Главной отличительной особенностью такого ряда является возможность применения для аппроксимации как выпуклых, так и многоэкстремальных одно- и двумерных функций, свойственных для передаточных характеристик оптических элементов.

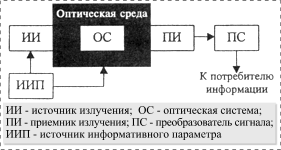
Преимущества выбранного метода можно пояснить на примере типового оптоэлектронного преобразователя. Обобщенную структуру любого оптоэлектронного измерительного устройства можно представить (рис. 1) в виде источника излучения (ИИ), приемника излучения (ПИ) с последующим преобразователем сигнала (ПС) и оптической средой, пропускающей излучение от источника к приемнику излучения [1-3]. При этом воздействие информативных параметров может осуществляться как на источник излучения, так и на оптическую среду, включающую в себя оптическую систему (ОС).

Рис. 1. Обобщенная структурная схема оптоэлектронного устройства

Например, в устройствах гальванической развязки аналоговых сигналов (оптронах) воздействие информативного параметра происходит посредством управления режимом работы ИИ, а в оптоэлектронных аналого-цифровых датчиках перемещения – путем пространственной модуляции ОС.

Во всех случаях изменение условий эксплуатации сказывается как на характеристиках источников излучения (для светодиодных ИИ температурный коэффициент изменения мощности излучения доходит до 1,5-2%/°С), так и на характеристиках оптической среды, а также приемников излучения. Во многих случаях изменением параметров оптической среды можно пренебречь.

Часто для уменьшения потерь в оптической среде на поверхности ИИ, ПИ и ОС (линзы, делители светового потока и др.) наносятся тонкопленочные просветляющие покрытия. Получившиеся комбинированные элементы многокомпонентных оптронных структур обладают совершенно иными спектральными, пространственными и температурными характеристиками. Например, полученные в результате просветления температурные характеристики МОС в значительной мере отличаются от исходных, а для полупроводниковых ИИ – существенно ухудшаются.

Проведенные экспериментальные исследования элементов МОС позволяют с высокой степенью точности представить их энергетические и спектральные характеристики в следующем виде:

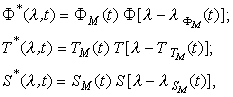(1)

где , , , , , – абсолютные и относительные спектральные характеристики мощности излучения ИИ, пропускания оптической среды и чувствительности ПИ соответственно; , , – температурные зависимости максимумов излучения ИИ, пропускания оптической среды и чувствительности ПИ; , , – температурные зависимости длины волны максимума излучения ИИ, пропускания ОС, чувствительности ПИ; , – длина волны и температура соответственно.

Отметим, что практически независимо от физической природы элементов МОС наблюдается температурный сдвиг их спектральных характеристик.

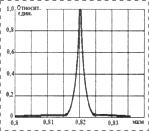
Так, например, температурная зависимость абсолютной спектральной характеристики излучения арсенидогалиевого инфракрасного диода (АЛ115, АЛ118 и др.) аппроксимируется одной функцией Гаусса:

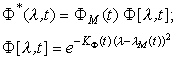, (2)

где – температурная зависимость полуширины спектральной характеристики; , – нижнее и верхнее значения температуры.

Погрешность аппроксимации составляет не более 4% в диапазоне температур –40...+80°С. Формирование аппроксимирующей функции (2) из двух гауссиан снижает погрешность аппроксимации почти в 10 раз – до 0,45%.

В общем случае аппроксимирующий ряд из функций Гаусса будет иметь вид

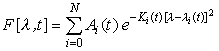, (3)

а в качестве критерия оптимальности аппроксимации можно использовать критерий минимума интегральной средней квадратической ошибки аппроксимации в заданном диапазоне температур :

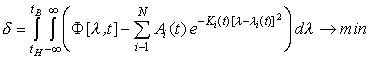. (4)

Разработан алгоритм и программа решения уравнения (4) методом Гаусса-Зейделя.

В таблице 1 приведены результаты аппроксимации некоторых тестовых функций рядом гауссиан и сравнения их с результатами аппроксимации тригонометрическим рядом Фурье, выбранным в качестве эталонного. Как видно из таблицы, для многих функций число членов и погрешность аппроксимации рядом гауссиан значительно ниже, чем рядом Фурье.

Таблица 1. Аппроксимация тестовых функций рядом Фурье и рядом гауссиан

№ п/п	Аппроксимируемая функция	Вид аппроксимируемой функции	Аппроксимирующий ряд	Средняя относительная погрешность	Число членов ряда
1.			Ряд гауссиан	0,1	8
2.			Ряд Фурье	0,04	12
3.			Ряд гауссиан	0,04	6
4.			Ряд Фурье	0,08	10
5.			Ряд гауссиан	0,009	4
6.			Ряд Фурье	0,1	8
7.	Спектральная характеристика ИК светодиода АЛ115А		Ряд гауссиан	0,095	3
8.			Ряд Фурье	0,01	110
9.	Спектральная характеристика светодиода АЛ341Е (желтый)		Ряд гауссиан	0,12	6
10.			Ряд Фурье		12
11.	Спектральная характеристика узкополосного интерференционного фильтра		Ряд гауссиан	0,023	6
12.			Ряд Фурье	0,11	13

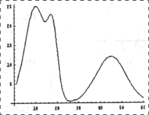
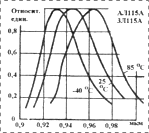
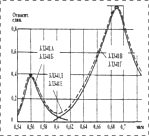
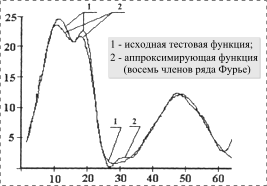
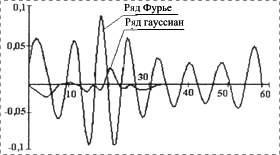
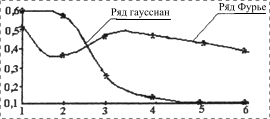
На рис. 2-4 в качестве примера представлены исходная тестовая функция (пп. 5 и 6 таблицы 1), результаты и погрешности аппроксимации рядом Фурье и рядом гауссиан, сравнительная зависимость погрешности аппроксимации от числа членов аппроксимирующих рядов.

Рис. 2. Аппроксимация тестовой функции рядом Фурье	Рис. 3. Погрешность аппроксимации (отн. ед.)

Рис. 4. Зависимость максимальной относительной погрешности иXTЂиXTЂ и от °.эла членов ряда

Как видно на этих рисунках, предложенный для практических расчетов ряд гауссиан достаточно эффективен при аппроксимации спектральных характеристик элементов МОС. Полученные выводы с высокой степенью достоверности распространяются также на пространственные характеристики источников и приемников излучения, функции пропускания различных компонентов оптической среды.

Список литературы

1. Порфирьев Л.Ф. Основы теории преобразования сигналов в оптико-электронных системах. Л.: Машиностроение, 1989. 387 с.

2. Конюхов Н.Е., Леонович Г.И., Матюнин С.А. Оптоэлектронные цифровые преобразователи перемещений с интерференционными элементами коррекции и обработки оптических сигналов // Приборы и системы управления. 1990. № 9. С. 18-20.

3. Матюнин С.А. Многокомпонентные оптоэлектронные аналоговые и аналого-цифровые преобразователи // Научно-техническая конференция “Датчик–2001”. Крым, Судак, 24-31 мая 2001.

4. Калиткин Н.Н. Численные методы. М.: Наука, 1978. 560 с.

5. Фильчаков П.Ф. Численные и графические методы прикладной математики: Справочник. Киев.: Наукова думка, 1970. 800с.

Наверх