УДК 621.382.017.71:621.384.3:519,3
А.А. Мельников, канд. техн. наук, доц.,
Московский
государственный институт радиотехники, электроники и автоматики (технический университет)
РАСЧЕТ ТЕМПЕРАТУРНЫХ ПОЛЕЙ В МНОГОСЛОЙНЫХ ФОТОПРИЕМНЫХ СТРУКТУРАХ
![]()
|
Предложена методика расчета температурных полей в многослойных фотоприемных структурах, иллюстрированная примером расчета тепловых режимов гибридного матричного фотоприемника ИК-диапазона на основе узкозонных твердых растворов CdxHg1-xTe (KTP). |
Обобщенные тепловые модели МФС
Математическая постановка задачи расчета температурных полей в МФС
Методика решения задач расчета температурных полей в МФС методом конечных элементов
Некоторые аспекты численного решения задач расчета температурных полей в МФС
Введение
Развитие полупроводниковой микроэлектроники стимулирует появление множества приборов, которые представляют собой сложные неоднородные многослойные конструкции. Это, например, фотоприемники и фотоприемные устройства для видимой, УФ- и ИК-областей спектра на основе различных полупроводниковых материалов (Si, Ge, GaAs, PbS, PbSe, InAs, CdxHg1-xTe). Разработка этих приборов невозможна без детального анализа их тепловых режимов.
Точные расчеты тепловых режимов работы многослойных фотоприемных структур (МФС), в состав которых входят детектирующая и считывающая структуры, в ряде практических случаев не могут быть выполнены из-за отсутствия приемлемых аналитических методов решения задач теплопередачи в этих структурах и ввиду сложности их конструктивных форм, характера граничных условий, разнообразия теплофизических характеристик применяемых полупроводниковых материалов, сложных законов распределения источников теплоты по объему структуры.
Поэтому актуальна проблема разработки эффективных численных методик расчета тепловых процессов в МФС. В основу разработанной численной методики расчета тепловых режимов МФС в настоящей статье положен метод конечных элементов (МКЭ).
Обобщенные тепловые модели МФС
Несмотря на многообразие конструктивных форм и функциональных особенностей фотоприемных структур можно предложить несколько обобщенных тепловых моделей, охватывающих широкий круг приложений.
Рассмотрим две такие обобщенные тепловые модели, из которых первая соответствует многослойной области без аномальных границ раздела сред, а вторая – многослойной области с аномальными границами раздела сред.
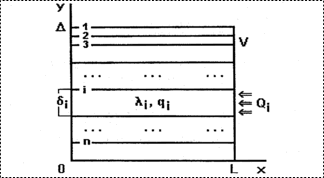
Обобщенная тепловая модель, представленная на рис. 1, включает целый ряд практических задач расчета температурных полей в монолитных МФС.
В монолитных МФС детектирующая и считывающая структуры изготовляются из одного полупроводникового материала.
Рассматриваемая область ![]() шириной
шириной ![]() и
толщиной
и
толщиной ![]() состоит из
состоит из ![]() слоев,
причем
слоев,
причем ![]() -й слой характеризуется толщиной
-й слой характеризуется толщиной ![]() ,
коэффициентом теплопроводности
,
коэффициентом теплопроводности ![]() . Источниками теплового
поля являются внутренние источники теплоты с удельной мощностью
. Источниками теплового
поля являются внутренние источники теплоты с удельной мощностью ![]() и
тепловые потоки на поверхности структуры с плотностью
и
тепловые потоки на поверхности структуры с плотностью ![]() . Модель,
изображенная на рис. 1, состоит из однородных параллельных слоев и не содержит
аномальных границ раздела сред, так как:
. Модель,
изображенная на рис. 1, состоит из однородных параллельных слоев и не содержит
аномальных границ раздела сред, так как:
· все границы слоев совпадают с
одноименным семейством координатных поверхностей ![]() ;
;
· теплопроводность слоев ![]() не
изменяется вдоль указанных границ.
не
изменяется вдоль указанных границ.
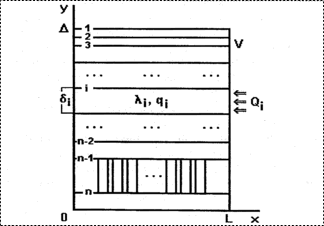
Обобщенная тепловая модель, изображенная на рис. 2, относится к гибридным МФС. В этих структурах детектирующая и считывающая структуры изготовляются из различных материалов.
|
|
|
| Рис. 1. Обобщенная тепловая модель МФС без аномальных границ раздела сред | Рис. 2. Обобщенная тепловая модель МФС с аномальными границами раздела сред |
Эта модель
содержит две аномальные границы раздела сред, являющиеся границами раздела слоев
![]() ,
, ![]() и
и
![]() ,
,
![]() (на этих границах зависимость теплопроводности
от координаты
(на этих границах зависимость теплопроводности
от координаты ![]() имеет ступенчатый
вид). Такие границы характерны, например, для гибридных матричных фотоприемников
ИК-диапазона.
имеет ступенчатый
вид). Такие границы характерны, например, для гибридных матричных фотоприемников
ИК-диапазона.
Математическая постановка задачи расчета температурных полей в МФС
В наиболее общем виде температурное поле в МФС, обобщенные тепловые модели которых представлены на рис. 1 и рис. 2, определяется из уравнения теплопроводности
![]() (1)
(1)
при граничных условиях
![]() на
на ![]() ;
(2)
;
(2)
![]() на
на ![]() ;
(3)
;
(3)
![]() на
на ![]() ;
(4)
;
(4)
и начальном условии
![]() при
при ![]() . (5)
. (5)
Кроме
этого, температурное поле в МФС удовлетворяет условиям сопряжения на границах
раздела слоев ![]() и
и
![]() :
:
![]() ; (6)
; (6)
![]() ,
(7)
,
(7)
где ![]() – температура;
– температура;
![]() – плотность материала;
– плотность материала; ![]() – теплоемкость;
– теплоемкость; ![]() – коэффициент
теплопроводности;
– коэффициент
теплопроводности; ![]() – удельная мощность источников теплоты, которая
считается положительной, если теплота подводится к структуре;
– удельная мощность источников теплоты, которая
считается положительной, если теплота подводится к структуре; ![]() –
поток теплоты на части границы
–
поток теплоты на части границы ![]() , который считается положительным,
если теплота теряется структурой;
, который считается положительным,
если теплота теряется структурой; ![]() – коэффициент
теплообмена с окружающей средой с температурой
– коэффициент
теплообмена с окружающей средой с температурой ![]() ;
; ![]() –
температура на части границы
–
температура на части границы ![]() ;
; ![]() –
начальное распределение температуры;
–
начальное распределение температуры; ![]() – полная граница
многослойной области
– полная граница
многослойной области ![]() ;
; ![]() – внешняя нормаль
к границе
– внешняя нормаль
к границе ![]() .
.
Модель (1)–(7) является математической моделью для расчета температурных полей в МФС. При расчете температурных полей в МФС мы будем пользоваться частными моделями, соответствующими общей. Отметим также, что в ряде практических случаев на боковых поверхностях тепловых моделей, представленных на рис. 1 и 2, имеет место условие адиабатичности.
Поэтому вместо граничного условия (4) можно использовать граничное условие
![]() .
(8)
.
(8)
Если температурное поле в МФС стационарно, т.е. процесс установившийся, то уравнение (1) преобразуется к виду
![]() .
(9)
.
(9)
В случае, когда теплофизические характеристики являются только функциями декартовых координат, из (9) получаем
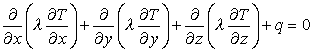 .
(10)
.
(10)
Это уравнение имеет вид
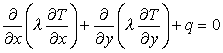 .
(11)
.
(11)
Уравнение (11) применяется для решения двумерных задач расчета температурных полей в МФС с плоскостной симметрией при следующих граничных условиях:
![]() на
на ![]() ;
(12)
;
(12)
![]() на
на ![]() ;
(13)
;
(13)
![]() на
на ![]() ;
(14)
;
(14)
и условиях сопряжения
на границе раздела слоев ![]() и
и ![]() (6), (7).
(6), (7).
Таким
образом, задача расчета температурных полей в МФС сводится к решению сопряженной
задачи теплопроводности при разнородных граничных условиях, заданных на различных
участках границы ![]() многослойной
области
многослойной
области ![]() .
.
Методика решения задач расчета температурных полей в МФС методом конечных элементов
В основу методики решения краевой задачи (11-14), (6-7) положен МКЭ. Можно показать, что решение этой задачи эквивалентно минимизации функционала [1]
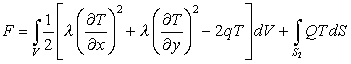 .
(15)
.
(15)
Для упрощения дальнейших преобразований введем матрицы
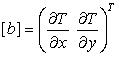 .
(16)
.
(16)
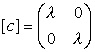 .
(17)
.
(17)
С учетом обозначений (16), (17) функционал (15) после преобразований можно записать в виде
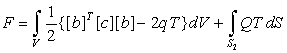 .
(18)
.
(18)
Предположим далее, что область ![]() разбита
на непересекающиеся конечные элементы с системой базисных функций
разбита
на непересекающиеся конечные элементы с системой базисных функций ![]() ,
,
![]() . Введем в рассмотрение функции
. Введем в рассмотрение функции ![]() ,
определенные на отдельных конечных элементах. Элементарный вклад конечного элемента
,
определенные на отдельных конечных элементах. Элементарный вклад конечного элемента
![]() в общие значения функционала (18)
определяется равенством
в общие значения функционала (18)
определяется равенством
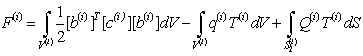 .
(19)
.
(19)
С учетом (19) выражение (18) можно переписать следующим образом:
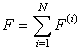 , (20)
, (20)
где
![]() – общее
число элементов, на которые разбита многослойная область
– общее
число элементов, на которые разбита многослойная область ![]() .
.
Для
того чтобы минимизировать функционал ![]() , необходимо
продифференцировать выражение (18) по
, необходимо
продифференцировать выражение (18) по ![]() и результат
приравнять нулю:
и результат
приравнять нулю:
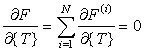 ,
(21)
,
(21)
где ![]() – узловые
значения искомой функции
– узловые
значения искомой функции ![]() . Искомая функция
. Искомая функция
![]() может
быть определена для каждого конечного элемента через базисные функции
может
быть определена для каждого конечного элемента через базисные функции ![]() следующим образом:
следующим образом: ![]() .
.
Таким образом,
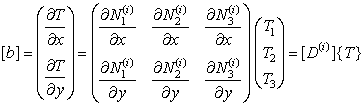 .
(22)
.
(22)
После дифференцирования выражения (20) по ![]() с
учетом выражений (19) и (22) и приравнивания результата нулю получим систему уравнений:
с
учетом выражений (19) и (22) и приравнивания результата нулю получим систему уравнений:
![]() , (23)
, (23)
где
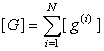 ;
(24)
;
(24)
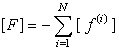 ; (25)
; (25)
![]() ;
(26)
;
(26)
![]() .
(27)
.
(27)
Для учета граничных условий Дирихле (12) систему уравнений
(23) преобразуем с помощью следующего алгоритма. Пусть для определенности задано
числовое значение температуры ![]() , тогда все преобразования
матричного уравнения (23) сводятся к следующему: все коэффициенты
, тогда все преобразования
матричного уравнения (23) сводятся к следующему: все коэффициенты ![]() -й
строки матрицы
-й
строки матрицы ![]() , за исключением диагонального, приравниваются
нулю,
, за исключением диагонального, приравниваются
нулю, ![]() -я компонента вектора
-я компонента вектора ![]() заменяется
на произведение
заменяется
на произведение ![]() ; все остальные уравнения преобразуются
вычитанием произведения
; все остальные уравнения преобразуются
вычитанием произведения ![]() из
из ![]() . и подстановкой
. и подстановкой
![]() ,
, ![]() ;
; ![]() .
.
Некоторые аспекты численного решения
задач
расчета температурных полей в МФС
Расчет температурного поля в МФС включает три этапа:
· описание геометрии, физических характеристик, генерацию конечно-элементной сетки;
· расчет с помощью МКЭ;
· визуализация и интерпретация результатов расчета.
Эти три этапа на уровне программного обеспечения выполняются отдельными модулями:
· модулем ввода данных (препроцессором);
· модулем вычислений (процессором счета);
· модулем вывода результатов (постпроцессором).
Препроцессор предназначен для ввода и подготовки информации, необходимой для решения задачи расчета температурного поля в МФС на ПЭВМ методом конечных элементов. Он осуществляет следующие функции:
· описание геометрии МФС;
· генерацию конечно-элементной сетки;
· указание областей и границ.
Генерация конечно-элементной сетки в области заключается в формировании совокупности узлов и совокупности конечных элементов, обеспечивающих приемлемую дискретизацию области. Узлы определяются координатами, тогда как элементы характеризуются типом и перечнем узлов.
Операция указания областей и границ позволяет уточнить следующую информацию:
· описание физических характеристик материалов;
· описание источников;
· описание граничных условий.
Процессор счета получает на входе описание конечно-элементной сетки, физические характеристики и граничные условия, а на выходе выдает значения искомых величин в каждом узле сети. Модуль вычислений выполняет следующие функции:
· построение подматриц и подвекторов на каждом конечном элементе;
· объединение этих подматриц и подвекторов для формирования матрицы и правой части линейной системы уравнений;
· учет граничных условий;
· решение линейной системы уравнений.
Постпроцессор выполняет следующие функции:
· извлекает значащую информацию;
· представляет численную информацию в графической форме для облегчения ее восприятия и интерпретации.
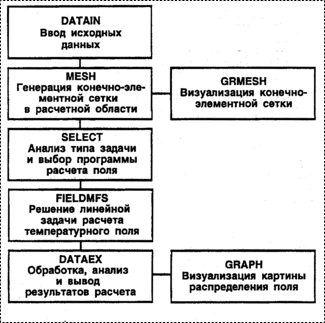
Схема алгоритма расчета температурных полей в МФС представлена на рис. 3, а структура комплекса программ расчета – на рис. 4.
|
|
|
| Рис. 4. Структура комплекса программ расчета температурных полей в МФС методом конечных элементов | |
| Рис. 3. Схема алгоритма расчета температурных полей в МФС |
|
Комплекс программ состоит из отдельных пакетов программ, каждый из которых выполняет вполне определенные функции. Пакет программ MESH предназначен для генерации конечно-элементной сетки в расчетной области, пакет F1ELDMFS – для решения задач расчета распределения температурных полей в МФС, пакет GRAPH – для визуализации результатов расчета в виде картин распределения температурных полей и т.д.
Для решения системы уравнений (15), полученной в результате дискретной аппроксимации по МКЭ сопряженной краевой задачи (1)–(5), использован метод треугольника разложения.
Исследование тепловых режимов
работы гибридной МФС ИК-диапазона
на основе твердых растворов CdxHg1-xTe (KPT)
|
|
|
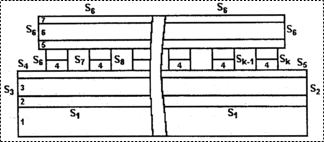
Рис. 5. Расчетная схема гибридной МФС: |
С
помощью разработанного комплекса программ были рассчитаны температурные режимы
работы гибридной МФС (рис. 5) с учетом геометрических размеров кристаллов, индиевых
межсоединений, тепловыделений в кремниевой интегральной схеме (ИС), первичной
обработки сигнала и известных теплопритоках через границы ![]() и
и ![]() .
.
Расчет проводился для матричного фотоприемника с размером кристалла фотодиодной матрицы 7´7 мм и размером кристалла кремниевой ИС 10´10 мм. Высота индиевых межсоединений составляла 10 мкм при площади их сечений 50´50 мкм, теплофизические константы материалов МФП брались из работ [2, 3].
Решалось уравнение теплопроводности (11) с граничными условиями
![]() на
на ![]() ; ,
(28)
; ,
(28)
![]() на
на ![]() ,
, ![]() ;
(29)
;
(29)
![]() на
на ![]() (30)
(30)
и
условиях сопряжения границ раздела слоев ![]() и
и ![]() (6), (7).
(6), (7).
В результате расчетов были получены зависимости максимальной температуры рабочего слоя КРТ от тепловыделений в кремниевой ИС, от теплопроводности клея, от теплопритоков через проволочные межсоединения кремниевой ИС с выводами корпуса и от рассогласования индиевых столбиков-контактов. Результаты расчетов показаны на соответствующих рисунках.
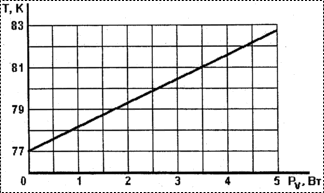
На рис. 6–9 показаны графики зависимости максимальной
температуры рабочего слоя КРТ: от тепловыделений в кремниевой ИС при мощности
теплопритоков через проволочные межсоединения кремниевой ИС с выводами корпуса
![]() ,
толщине клеевого слоя
,
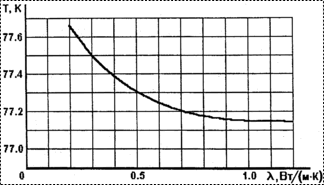
толщине клеевого слоя ![]() (рис. 6); от теплопроводности клея
при мощности, выделяемой в кремниевой ИС, равной 0,5 Вт, мощности теплопритоков
через проволочные межсоединения кремниевой ИС с выводами корпуса
(рис. 6); от теплопроводности клея
при мощности, выделяемой в кремниевой ИС, равной 0,5 Вт, мощности теплопритоков
через проволочные межсоединения кремниевой ИС с выводами корпуса ![]() Вт,
Вт,
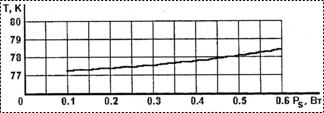
![]() мкм (рис. 7); от мощности теплопритоков
через проволочные межсоединения кремниевой ИС с выводами корпуса при
мкм (рис. 7); от мощности теплопритоков
через проволочные межсоединения кремниевой ИС с выводами корпуса при ![]() Вт,
Вт,
![]() мкм,
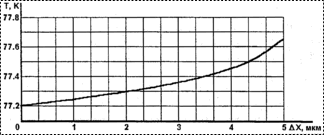
мкм, ![]() Вт/(м×К) (рис. 8); от рассогласования индиевых
столбиков-контактов при
Вт/(м×К) (рис. 8); от рассогласования индиевых
столбиков-контактов при ![]() Вт,
Вт, ![]() мкм,
мкм,
![]() Вт/(м×К)
(рис. 9).
Вт/(м×К)
(рис. 9).
|
|
|
| Рис. 6. Зависимость максимальной температуры рабочего слоя КРТ от тепловыделений в кремниевой ИС |
Рис. 7. Зависимость максимальной температуры
рабочего слоя КРТ |
|
|
|
| Рис. 8. Зависимость максимальной температуры рабочего слоя КРТ от теплопритоков через проволочные межсоединения кремниевой ИС с выводами корпуса |
Рис. 9. Зависимость максимальной температуры рабочего слоя КРТ от рассогласования индиевых столбиков-контактов |
|
|
|
Рис. 10. Распределение температуры в рабочем слое КРТ |
На рис. 10 приведено распределение температурного поля
в рабочем слое КРТ при ![]() Вт,
Вт, ![]() мкм,
мкм, ![]() Вт/(м×К),
Вт/(м×К), ![]() Вт.
Вт.
Результаты расчетов показали, что рассогласование индиевых столбиков-контактов при сборке гибридных многослойных фотоприемных структур не должна превышать 3 мкм, в противном случае рабочий слой КРТ будет иметь недопустимо высокую температуру, так как ухудшается его охлаждение.
* * *
Использование разработанной методики позволяет отказаться от дорогостоящих и часто невозможных экспериментов, определить целесообразность той или иной технологии изготовления приборов и устройств на основе многослойных структур, повысить качество и надежность изделий микросистемной техники.
Список
литературы
1. Melnikov A.A., Kulchitsky N.A. and Khryapov V.T. Temperature field mathematical modeling in multilayer semiconductor structures being produced and functioning in microgravity // Hydromechanics and Heat/Mass Transfer in Microgravity Reviewed Proceedings of the First International Symposium on Hydromechanics and Heat/Mass Transfer in Microgravity Gordon and Breach Science Publishers. 1992. P. 363-366.
2. Берченко Н.Н., Крсвс В.Е., Средин В.Г. Полупроводниковые твердые растворы и их применение, М.: Воениздат, 1982.
3. Охотин А.С., Пушкарский А.С., Горбачев В.В. Теплофизические свойства полупроводников, М.: Атомиздат, 1972. 200 с.