УДК 004.383.4:681.7.069.2
В.А.Васильев, канд. физ.-мат. наук, Пензенский государственный университет
Информационная модель взаимодействия оптического излучения с полупроводниковой структурой
![]()
|
Рассмотрен процесс создания
информационного ресурса взаимодействия оптического излучения с полупроводниковой
структурой. Представлена модель воссоздания спектров оптического пропускания
и отражения полупроводниковых структур, основанная на матричном формализме.
Показана возможность получения информации о характеристиках многослойных
полупроводниковых структур из экспериментальных спектров оптического отражения
путем их моделирования. |
Для представления информации об объектах той или иной природы используют различные информационные модели, включающие стандартные параметры (характеристики) конкретных объектов. В целом информационная модель должна обеспечивать создание и/или обнаружение информации, ее регистрацию и оценку. Перечисленные требования согласно [1,2] являются этапами создания информационного ресурса. В работе [3] информационный ресурс определен как симбиоз знаний и информации. Информационная модель, построенная на основе знаний об объекте (свойств, параметров, характеристик и др.), знаний законов взаимодействия объекта с другими объектами, средами и полями, позволяет извлекать информацию об объекте, содержащуюся в зарегистрированном сигнале, и тем самым создавать информационный ресурс.
Большой научный и практический интерес представляют вопросы создания и изучения информационного ресурса взаимодействия оптического излучения с полупроводниковой структурой. Откликом такого взаимодействия являются оптические спектры (отражения, пропускания и др.), которые несут в себе достаточно большое количество информации. Знание законов изменения и методов анализа спектров позволяет не только обнаружить, зарегистрировать, но и оценить качественные и количественные характеристики исследуемого объекта. Соединение оптических спектральных методов создания/обнаружения с методами анализа информационных ресурсов открывает новые возможности в изучении полупроводниковых структур [4].
Процесс создания информационного ресурса взаимодействия оптического излучения с полупроводниковой структурой состоит из следующих этапов.
1. Создание и/или обнаружение информации:
![]() ,
(1)
,
(1)
где ![]() – информационное поле;
– информационное поле;
![]() – информационная
обстановка;
– информационная
обстановка; ![]() – ресурсосоздающие
параметры;
– ресурсосоздающие
параметры; ![]() – преобразование поля,
выделяющее созданную и/или обнаруженную информацию;
– преобразование поля,
выделяющее созданную и/или обнаруженную информацию; ![]() – параметр преобразования
выделения созданной и/или обнаруженной информации.
– параметр преобразования
выделения созданной и/или обнаруженной информации.
2. Регистрация информации:
![]() ,
(2)
,
(2)
где ![]() – преобразование
регистрации;
– преобразование
регистрации; ![]() – параметр
преобразования регистрации.
– параметр
преобразования регистрации.
3. Извлечение и/или распознавание информации:
![]() ,
(3)
,
(3)
где ![]() – преобразование
распознавания;
– преобразование
распознавания; ![]() – параметр
преобразования распознавания.
– параметр
преобразования распознавания.
Преобразование извлечения/распознавания представляет собой получение скрытых и дополнительных параметров, которые несет в себе зарегистрированный сигнал (например, зарегистрированный спектр отражения полупроводниковой структуры, спектр пропускания и т.п.).
4. Оценивание информации:
![]() , (4)
, (4)
где ![]() – преобразование
оценки;
– преобразование
оценки; ![]() – параметр
преобразования оценки.
– параметр
преобразования оценки.
Преобразование оценки относится как к оцениванию непосредственно качества информации (характеристик обнаружения, точности измерения и т.д.), так и к оцениванию стоимости ее создания, обнаружения, регистрации и т. п. и представляет собой сложную структуру.
5. Определение закона деградации для данного вида информации (по аналогии с [5]):
![]() ,
(5)
,
(5)
где ![]() – преобразование
деградации;
– преобразование
деградации; ![]() – параметр преобразования
деградации.
– параметр преобразования
деградации.
Деградация (ухудшение) информации может происходить как за счет естественного снижения информационной эффективности системы с увеличением времени работы системы, так и под воздействием дестабилизирующих факторов.
6. Определение закона обновления информации (подобно [5]):
![]() ; (6)
; (6)
![]() , (7)
, (7)
где ![]() ,
, ![]() – преобразования
обновления;
– преобразования
обновления; ![]() ,
, ![]() – параметры
преобразования обновления.
– параметры
преобразования обновления.
Закон обновления информации может быть выведен на основе применения
показателя информационной эффективности ![]() :
:
![]() ,
(8)
,
(8)
где ![]() – относительное
изменение параметра от предельно допустимого;
– относительное
изменение параметра от предельно допустимого; ![]() – относительное изменение текущей реализации фактора
– относительное изменение текущей реализации фактора ![]() (
(![]() ) от выбранного значения фактора L в интервале от
) от выбранного значения фактора L в интервале от ![]() до
до ![]() (конечное значение).
(конечное значение).
Нахождение конкретного вида ![]() и
и ![]() является одной из
задач теории информационных ресурсов (ИР) [1].
является одной из
задач теории информационных ресурсов (ИР) [1].
Для нахождения ![]() и
и ![]() в случае
взаимодействия оптического излучения с полупроводниковой структурой необходимо
знание физических процессов, протекающих в полупроводниковых структурах, особенностей
взаимодействия твердого тела с электромагнитным излучением, законов изменения и
методов анализа спектров. С этой точки зрения несомненный интерес
представляют разработка и исследование новых моделей и алгоритмов анализа
данных оптических спектральных измерений полупроводниковых структур.
в случае
взаимодействия оптического излучения с полупроводниковой структурой необходимо
знание физических процессов, протекающих в полупроводниковых структурах, особенностей
взаимодействия твердого тела с электромагнитным излучением, законов изменения и
методов анализа спектров. С этой точки зрения несомненный интерес
представляют разработка и исследование новых моделей и алгоритмов анализа
данных оптических спектральных измерений полупроводниковых структур.
В диапазоне длин волн от 10 до 1000 см-1
(длинноволновая часть оптического диапазона) из экспериментальных спектров
оптического отражения путем их искусственного воссоздания (моделирования на
ЭВМ) можно определять важные параметры и характеристики полупроводников:
плазменную частоту ![]() , частоту поперечных оптических фононов
, частоту поперечных оптических фононов ![]() , концентрацию свободных носителей заряда
, концентрацию свободных носителей заряда ![]() и подвижность
свободных носителей заряда
и подвижность
свободных носителей заряда ![]() . Кроме того, по спектрам длинноволнового оптического
отражения можно определять толщины тонких полупроводниковых и диэлектрических
слоев [6].
. Кроме того, по спектрам длинноволнового оптического
отражения можно определять толщины тонких полупроводниковых и диэлектрических
слоев [6].
При исследовании
длинноволновых возбуждений кристалл можно рассматривать как непрерывную среду.
Макроскопическая теория длинноволновых оптических колебаний решетки в ионных
кристаллах была впервые развита Хуаном Кунем [7]. Она
основана на том, что длинноволновые колебания в ионных кристаллах, содержащих
по два иона в элементарной ячейке, связаны с относительным смещением подрешеток
положительных и отрицательных ионов. Рассмотрение уравнения движения для случая
продольных и поперечных колебаний ионов позволяет получить простое соотношение
между частотами продольных ![]() и поперечных
и поперечных ![]() колебаний:
колебаний:
![]() ,
(9)
,
(9)
где ![]() – статическая
диэлектрическая проницаемость;
– статическая
диэлектрическая проницаемость; ![]() – диэлектрическая
проницаемость на бесконечной частоте.
– диэлектрическая
проницаемость на бесконечной частоте.
Согласно модели диэлектрической проницаемости (учитывающей ангармонические эффекты), предложенной Хуаном Кунем, коэффициент преломления может быть определен по формуле
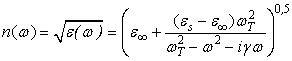 ,
(10)
,
(10)
где ![]() – параметр затухания.
– параметр затухания.
В области частот ![]() действительная часть диэлектрической
проницаемости
действительная часть диэлектрической
проницаемости ![]() отрицательна, а комплексный показатель
преломления
отрицательна, а комплексный показатель
преломления ![]() является чисто мнимой
величиной.
является чисто мнимой
величиной.
Если энергия фотона мала по сравнению с шириной запрещенной зоны, то существенным оказывается взаимодействие электромагнитного излучения со свободными носителями заряда. Оптическая электропроводность согласно Друде [8] определяется по формуле
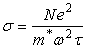 ,
(11)
,
(11)
где ![]() – концентрация свободных
носителей заряда;
– концентрация свободных
носителей заряда; ![]() – эффективная масса
носителей заряда;
– эффективная масса
носителей заряда; ![]() – время релаксации;
– время релаксации; ![]() – заряд электрона.
– заряд электрона.
Коэффициент преломления в этом случае
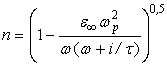 , (12)
, (12)
где ![]() – плазменная частота;
– плазменная частота; 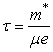 ;
; ![]() – подвижность
носителей заряда.
– подвижность
носителей заряда.
Электромагнитные волны могут
распространяться в среде, только если действительная часть диэлектрической
проницаемости положительна; в случае же, когда ее значение отрицательно,
электромагнитная волна полностью отражается. Плазменная частота ![]() отделяет область пропускания
от области полного отражения и может быть определена в соответствии с (11) по
формуле
отделяет область пропускания
от области полного отражения и может быть определена в соответствии с (11) по
формуле
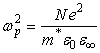 .
(13)
.
(13)
Выражение (13) можно использовать для большинства полупроводников, так как в
полупроводниках ![]() -типа проводимости время релаксации
-типа проводимости время релаксации ![]() можно считать не
зависящим от энергии носителя, поскольку электроны в зоне проводимости обладают
большой подвижностью и малой эффективной массой.
можно считать не
зависящим от энергии носителя, поскольку электроны в зоне проводимости обладают
большой подвижностью и малой эффективной массой.
С учетом вкладов решеточных и плазменных колебаний коэффициент преломления может быть определен по формуле
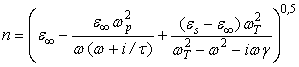 .
(14)
.
(14)
Если решеточных осцилляторов несколько, то выражение (14) приобретает вид
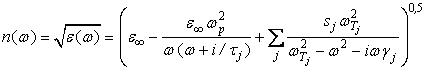 . (15)
. (15)
где ![]() – высокочастотная
диэлектрическая проницаемость;
– высокочастотная
диэлектрическая проницаемость; ![]() – плазменная частота;
– плазменная частота; ![]() –- частота
–- частота ![]() -го поперечного оптического фонона;
-го поперечного оптического фонона; ![]() – текущая частота;
– текущая частота; ![]() – сила
– сила ![]() -го осциллятора;
-го осциллятора; ![]() – время релаксации;
– время релаксации; ![]() – параметр затухания.
– параметр затухания.
В случае твердого раствора высокочастотная диэлектрическая проницаемость ![]() может быть определена
линейной интерполяцией соответствующих значений компонентов. Силы осцилляторов
можно рассчитать по формуле
может быть определена
линейной интерполяцией соответствующих значений компонентов. Силы осцилляторов
можно рассчитать по формуле
![]() ,
(16)
,
(16)
где ![]() ,
, ![]() – высокочастотная и
низкочастотная диэлектрические проницаемости;
– высокочастотная и
низкочастотная диэлектрические проницаемости; ![]() – мольная доля компонента.
– мольная доля компонента.
Моделирование спектров оптического отражения полупроводников и полупроводниковых структур может быть основано на модели коэффициента преломления (диэлектрической проницаемости) (15).
В ряде случаев требуется определение коэффициентов отражения и пропускания неоднородных полупроводниковых структур. Для описания спектров оптического отражения полупроводниковых структур, представляющих собой эпитаксиальный слой на подложке, может использоваться однослойная модель. В этом приближении коэффициент отражения со стороны подложки определяется по формуле [9]
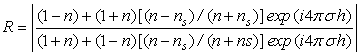 , (17)
, (17)
где ![]() ,
, ![]() – коэффициенты
преломления слоя и подложки;
– коэффициенты
преломления слоя и подложки; ![]() – толщина слоя;
– толщина слоя; ![]() а – волновое число;
а – волновое число; ![]() .
.
Наиболее удобным для моделирования спектров оптического отражения и пропускания полупроводниковых структур является матричный метод. Матричный метод в применении к диэлектрическим слоям описан в работе [10]. С его помощью представляется возможным учитывать неоднородность твердотельных структур, разбивая их на отдельные однородные слои и описывая каждый слой характеристической матрицей.
Если
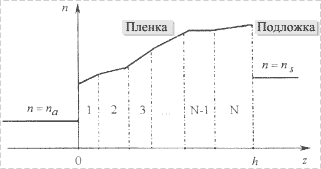
многослойная структура состоит из ![]() слоев (рис. 1),
то матрица
слоев (рис. 1),
то матрица ![]() для области,
заключенной между
для области,
заключенной между ![]() и
и ![]() , равна произведению матриц
, равна произведению матриц ![]() для этих слоев:
для этих слоев:
 ,
(18)
,
(18)
|
|
|
Рис. 1. Схема профиля показателя |
Коэффициенты отражения и пропускания по напряженности
поля выражаются через матричные элементы матрицы ![]() :
:
![]() ; (19)
; (19)
![]() . (20)
. (20)
Коэффициенты отражения и пропускания по интенсивности определяются по формулам
![]() ;
; ![]() .
(21)
.
(21)
На практике часто используются слои, имеющие градиент коэффициента преломления, который может быть обусловлен особенностями эпитаксиального роста и процессов диффузии или создан намеренно для обеспечения требуемых характеристик структуры. Для описания таких структур может быть использовано гиперболическое распределение коэффициента преломления:
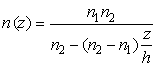 , (22)
, (22)
где ![]() – коэффициент преломления;
– коэффициент преломления; ![]() и
и ![]() – значения коэффициента преломления на
границах слоя;
– значения коэффициента преломления на
границах слоя; ![]() – толщина слоя.
– толщина слоя.
Данное распределение удобно
тем, что при малых ![]() – оно практически
линейно и позволяет при использовании матричного формализма записать
характеристическую матрицу слоя в аналитическом виде:
– оно практически
линейно и позволяет при использовании матричного формализма записать
характеристическую матрицу слоя в аналитическом виде:
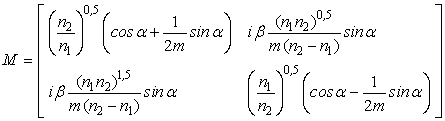 , (23)
, (23)
где 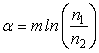 ;
; 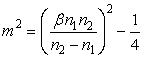 ;
; ![]() ;
; ![]() – волновое
число;
– волновое
число; ![]() – толщина слоя;
– толщина слоя; ![]() .
.
В частном случае однородного
слоя (![]() ) характеристическая матрица имеет вид
) характеристическая матрица имеет вид
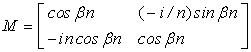 . (24)
. (24)
Подстановкой (14) в (16)
получается коэффициент отражения по интенсивности, выраженный через матричные
элементы ![]() матрицы
матрицы ![]() :
:
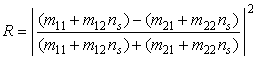 , (25)
, (25)
где ![]() – коэффициент преломления подложки.
– коэффициент преломления подложки.
На практике часто используются многослойные структуры и слои, имеющие градиент состава, концентрации и подвижности свободных носителей заряда, которые могут быть обусловлены особенностями эпитаксиального роста и процессов диффузии или созданы намеренно для обеспечения требуемых характеристик структуры.
|
|
|
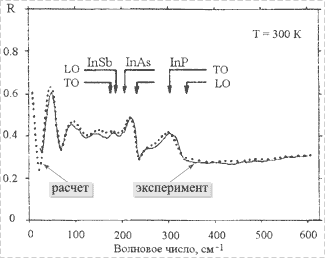
Рис.
2. Спектр оптического отражения |
На рис. 2 показан спектр оптического отражения эпитаксиальной
полупроводниковой структуры ![]() -InAs0,63Sb0,12P0,25 : Zn /
-InAs0,63Sb0,12P0,25 : Zn / ![]() -InAs. Особенностью спектров отражения таких
структур является то, что они не поддаются описанию с помощью однослойной модели
из-за глубокого проникновения цинка (Zn) в подложку в процессе диффузии. Для описания спектров
оптического отражения применялась двухслойная модель расчета. Коэффициент
преломления рассчитывался по формуле (15) при числе осцилляторов
-InAs. Особенностью спектров отражения таких
структур является то, что они не поддаются описанию с помощью однослойной модели
из-за глубокого проникновения цинка (Zn) в подложку в процессе диффузии. Для описания спектров
оптического отражения применялась двухслойная модель расчета. Коэффициент
преломления рассчитывался по формуле (15) при числе осцилляторов ![]() . Характеристические матрицы слоев и подложки определялись по
формуле (19), характеристическая матрица структуры – по формуле (13), коэффициент
отражения – по формуле (20). Значения параметров слоев, определенные в
результате процедуры подгонки теоретических спектров под экспериментальные
данные, приведены в таблице 1.
. Характеристические матрицы слоев и подложки определялись по
формуле (19), характеристическая матрица структуры – по формуле (13), коэффициент
отражения – по формуле (20). Значения параметров слоев, определенные в
результате процедуры подгонки теоретических спектров под экспериментальные
данные, приведены в таблице 1.
Таблица 1.
Параметры слоев полупроводниковой структуры ![]() -InAs0,63Sb0,12P0,25 : Zn /
-InAs0,63Sb0,12P0,25 : Zn / ![]() -InAs
-InAs
|
|
220 |
|
|
55 |
|
|
2,0 |
|
|
0,11 |
|
|
16 |
|
|
25 |
|
|
27 |
|
|
2,2 |
|
|
18 |
Первая цифра в индексе указывает номер слоя, вторая цифра в индексе – номер
осциллятора (для ![]() ). Заметим, что первый от поверхности слой представляет собой
твердый раствор, а второй слой образован в подложке за счет диффузии примеси Zn. Установлено, что толщина
первого слоя
). Заметим, что первый от поверхности слой представляет собой
твердый раствор, а второй слой образован в подложке за счет диффузии примеси Zn. Установлено, что толщина
первого слоя ![]() мкм, а толщина второго слоя
мкм, а толщина второго слоя ![]() мкм. Параметр
мкм. Параметр ![]() определяет период
осцилляции в части спектра ниже 200 см-1. Осцилляции являются
следствием интерференции в слое между областью объемного заряда и
эпитаксиальным слоем. По параметру
определяет период
осцилляции в части спектра ниже 200 см-1. Осцилляции являются
следствием интерференции в слое между областью объемного заряда и
эпитаксиальным слоем. По параметру ![]() можно судить о
положении
можно судить о
положении ![]() -
-![]() -перехода в структуре.
-перехода в структуре.
Несколько лучшее сходство теоретических и экспериментальных результатов (в сравнении с рис. 2 – примерно на 5%) достигается при использовании двухслойной модели с градиентными слоями, в которой применяется гиперболическое распределение (17) и характеристическая матрица (18).
Достоверность и точность параметров, получаемых из расчетной модели,
оценивалась по чувствительности к параметрам слоя ![]() ,
, ![]() ,
, ![]() и
и ![]() на примере структуры
на примере структуры ![]() -InAs0,63Sb0,12P0,25 : Zn /
-InAs0,63Sb0,12P0,25 : Zn / ![]() -InAs. К изменению плазменной
частоты
-InAs. К изменению плазменной
частоты ![]() расчетная модель имеет
достаточно высокую чувствительность. Причем наблюдается практически линейная
зависимость. Так, с изменением
расчетная модель имеет
достаточно высокую чувствительность. Причем наблюдается практически линейная
зависимость. Так, с изменением ![]() на 10% максимальное
значение коэффициента отражения
на 10% максимальное
значение коэффициента отражения ![]() тоже изменяется
приблизительно на 10%. Следует заметить, что наибольшее изменение коэффициента
отражения приходится на область частот решеточных колебаний и связано с плазмонфононным взаимодействием. Анализ
отклонений других параметров показывает, что время релаксации
тоже изменяется
приблизительно на 10%. Следует заметить, что наибольшее изменение коэффициента
отражения приходится на область частот решеточных колебаний и связано с плазмонфононным взаимодействием. Анализ
отклонений других параметров показывает, что время релаксации ![]() слабо влияет на
коэффициент отражения
слабо влияет на
коэффициент отражения ![]() и при изменении
и при изменении ![]() на 50% коэффициент отражения
меняется не более чем на 8%. Модель достаточно хорошо чувствительна к изменению
параметров
на 50% коэффициент отражения
меняется не более чем на 8%. Модель достаточно хорошо чувствительна к изменению
параметров ![]() и
и ![]() . Изменение
. Изменение ![]() на 50% приводит к
изменению коэффициента отражения до 15%, а изменение
на 50% приводит к
изменению коэффициента отражения до 15%, а изменение ![]() на 10% – к изменению
коэффициента отражения до 25%. Если в качестве нижнего предела чувствительности
взять приблизительно 3%, то получим оценки относительных погрешностей
определения параметров. Относительные погрешности определения параметров
полупроводникового слоя составляют: для
на 10% – к изменению
коэффициента отражения до 25%. Если в качестве нижнего предела чувствительности
взять приблизительно 3%, то получим оценки относительных погрешностей
определения параметров. Относительные погрешности определения параметров
полупроводникового слоя составляют: для ![]() – 3%, для
– 3%, для ![]() – 50%, для
– 50%, для ![]() – 5%, для
– 5%, для ![]() – 15% при выбранных
базовых значениях
– 15% при выбранных
базовых значениях ![]() см-1,
см-1, ![]() см,
см, ![]() ,
, ![]() мкм.
мкм.
Подгоночные параметры, полученные из расчетной модели и приведенные выше, в
конечном итоге позволяют получать информацию о таких важных характеристиках
полупроводника, как концентрация свободных носителей заряда ![]() и подвижность
и подвижность ![]() [11]. Значения
[11]. Значения ![]() и
и ![]() , получаемые из оптических спектров путем их моделирования,
достаточно хорошо коррелируют со значениями
, получаемые из оптических спектров путем их моделирования,
достаточно хорошо коррелируют со значениями ![]() и
и ![]() , получаемыми по результатам измерений ЭДС Холла.
, получаемыми по результатам измерений ЭДС Холла.
Список литературы
1. Бакут П.А., Шумилов Ю.П. Информационные технологии, информационные ресурсы, интеллектуальная собственность – понятия, взаимосвязь, проблемы // Информационные ресурсы России. 1997. № 5. С. 18-19.
2. Бакут П.А., Шумилов Ю.П. Информационные ресурсы – вопросы теории и практика // Информационные ресурсы России. 1999. № 3. С. 18-20.
3. Острейковский В.А. Информатика: Учеб. для вузов. М.: Высш. шк. 2000. 511 с.
4. Василев В.А. Оптические спектральные методы формирования информационных ресурсов твердотельных структур // XXVII Международная конференция “Информационные технологии в науке, образовании, телекоммуникации и бизнесе”. Труды конференции. Ялта, Гурзуф. 2000. С. 182-186.
5. Шумилов Ю.А. Методы создания и анализа информационных ресурсов оптических информационных систем. Докт. дис. М., 1998. 228 с.
6. Баранов А.Н., Васильев В.А., Копылов А.Н., Шерстнев В.В. Оптическое отражение и определение характеристик эпитаксиальных структур InAs1-x-ySbxPy / InAs // ФТП. 1991. Т. 25. Вып. 1. С. 99-101.
7. Борн М., Хуан Кунь. Динамическая теория кристаллических решеток. М., 1958. 488 с.
8. Анималу А. Квантовая теория кристаллических твердых тел. М.: Мир, 1981. 574 с.
9. Зингер Г.М., Ипатова И.П., Рыскин А.И. Оптические свойства четверных твердых растворов на основе соединений А3В5 в области решеточных и плазменных колебаний // ФТП. 1984. Т. 18. Вып. 1. С. 24-42.
10. Якобсон Р. Физика тонких пленок / Под ред. Г.Хасса, М.Франкомба и Р.Гофмана. М.: Мир, 1967. Т. 8. С. 91-151.
11. Васильев В.А. Методика определения параметров полупроводников по спектрам длинноволнового оптического отражения // Материалы V Международной научно-методической конференции “Университетское образование” (МКУО-2001). Пенза, 2001. Ч. 1. С. 70-72.
| Наверх |