УДК 621.317.772:681.325

В.М.Сапельников, д-р техн. наук, Р.А.Хакимов, Башкирский государственный университет

Функциональные цифроаналоговые преобразователи и калибраторы фазы на их основе

Рассмотрены два метода построения цифроаналоговых преобразователей с нелинейной характеристикой преобразования. Используются два способа аппроксимации: кусочно-линейная и степенная. Показана возможность построения цифроуправляемых калибраторов фазы на основе функциональных цифроаналоговых преобразователей.

Цифроаналоговые преобразователи (ЦАП) широко используются для преобразования сигналов в информационно-измерительной технике, радиотехнике и приборостроении. Они являются мощным средством увеличения точности отсчета. Особенно важно эти вопросы рассматривать в распределенных метрологических системах, разрабатываемых на основе микросистемной техники.

Существующие ЦАП могут выполнять только линейные преобразования вида [1,2]. В то же время в различных областях техники необходимо с высокой точностью воспроизводить нелинейные функциональные зависимости. Например, такая необходимость возникает при построении цифроуправляемых фазовращателей и калибраторов фазы, так как зависимость фазового сдвига от изменения регулируемой величины всегда нелинейна [3,4]. Наиболее предпочтительный способ для осуществления этой операции – использование ЦАП.

Для воспроизведения нелинейных функциональных зависимостей и моделирования их с помощью линейных ЦАП мы использовали два вида аппроксимации: кусочно-линейную аппроксимацию и аппроксимацию степенными рядами. Каждый из указанных видов аппроксимации предполагает свой способ аппаратной реализации. Однако оба способа для увеличения дискретности воспроизводимой функции используют стандартные многоразрядные ЦАП.

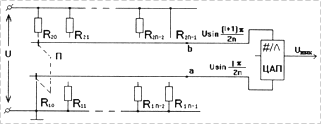
Рассмотрим первый способ (рис. 1), в котором используется линейная аппроксимация воспроизводимой функциональной зависимости в интервале . Здесь – отрезок аппроксимации функциональной зависимости , который разбивается на интервалы величиной ; – номер интервала аппроксимации; – число интервалов аппроксимации зависимости . Полагаем, что на отрезке аппроксимации функция неотрицательна, хотя данный способ может быть распространен и на отрицательные значения функции.

В качестве многоразрядного линейного ЦАП используется любой умножающий ЦАП с постоянным входным сопротивлением [2]. Это может быть ЦАП, использующий резисторную матрицу и управляемый двоичным кодом, или делитель напряжения с шунтирующими декадами, управляемый десятичным кодом.

Если предположить, что напряжение, подводимое к функциональному ЦАП, равно максимальному значению функции на участке , тогда сопротивления , , будут связаны между собой соотношениями:

;

.

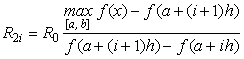Напряжения в схеме (рис. 1) при этом распределятся следующим образом:

; .

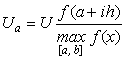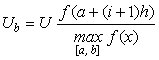Рис. 1. Функциональный ЦАП – дискретный аналог
синусного потенциометра

С помощью линейного ЦАП выходное напряжение изменяется от до , приближенно воспроизводя в -м интервале зависимость с заданным шагом квантования. Для изменения интервала регулирования функциональной зависимости (старший разряд функционального ЦАП) используется ключ .

Естественно, что при таком построении функционального ЦАП последний имеет методическую погрешность, вызванную линейной аппроксимацией функциональной зависимости в интервале . Эта погрешность определяется выражением

,

где – уравнение прямой, аппроксимирующей зависимость в интервале .

Введем обозначение , тогда уравнение прямой запишется в виде

.

Здесь .

Методическая погрешность воспроизведения функции будет зависеть как от ее вида и выбранного отрезка аппроксимации, так и от номера и чисел участков аппроксимации.

Функциональные ЦАП, аппроксимирующие функции и , широко применяются при построении калибраторов фазы и фазовращателей [3,4], в которых при формировании напряжения выхода реализуется соотношение

. (1)

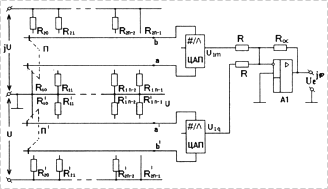
На рис. 2 приведена принципиальная схема калибратора фазы с поразрядным регулированием фазового сдвига. Схема состоит из двух функциональных ЦАП, моделирующих синусную и косинусную зависимости в интервале [0°,90°].

Ко входам устройства подводятся два синусоидальных напряжения, равных по модулю и сдвинутых по фазе на 90° (для регулирования фазового сдвига в одном квадранте). Эти напряжения подаются на функциональные ЦАП, которые с допустимой погрешностью воспроизводят зависимости и .

Для реализации соотношения (1) проводится суммирование выходных напряжений и с помощью операционного усилителя .

Кроме того, рассмотренный способ применим для построения цифроуправляемых потенциометрических и мостовых фазовращателей [4].

Второй способ, использующий степенную аппроксимацию, заключается в следующем. На рассматриваемом отрезке функция заменяется многочленом .

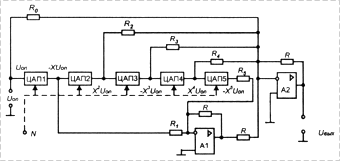
Моделирование многочлена осуществляется каскадно соединенными ЦАП (рис. 3).

Рис. 2. К принципу построения синусно- косинусного калибратора фазы	Рис. 3. Схема функционального цифроаналогового преобразователя

В качестве ЦАП, изображенных на схеме, применяют умножающие ЦАП, которые могут работать с двуполярным опорным напряжением. Выходное напряжение таких ЦАП определяется по формуле

,

где – текущий цифровой код, который изменяется в пределах от 0 до ; ; – разрядность ЦАП; – сопротивление матрицы резисторов; – сопротивление резистора цепи обратной связи операционного усилителя ЦАП; – опорное напряжение. Отношение называют масштабным коэффициентом, или масштабным множителем. Его можно изменять в широких пределах, изменяя значение .

В схеме, приведенной на рис. 3, при подаче на цифровые входы ЦАП кода на выходе ЦАП1 формируется напряжение

.

Это напряжение является входным для второго ЦАП, а напряжение на его выходе будет определяться соотношением

.

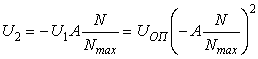Продолжая этот ряд, для -го ЦАП можно записать:

.

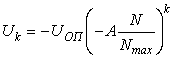Напряжения с выходов ЦАП через резисторы подаются на вход сумматора . Для обеспечения необходимого знака сигнала напряжения с выходов первого и пятого ЦАП проходят через инвертор . Дополнительно на сумматор через резистор подается опорное напряжение. На выходе сумматора формируется напряжение

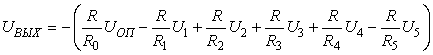
или (с учетом предыдущего уравнения)

.

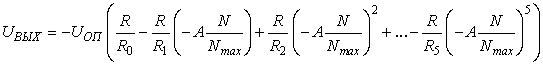Обозначим , , тогда последнее уравнение примет вид

.

Коэффициенты многочлена, реализуемого по данной схеме, имеют следующие знаки: , , , , . Если коэффициенты имеют другие знаки, то схема претерпевает лишь незначительные изменения. Таким образом, мы получаем выходное напряжение, пропорциональное аппроксимируемой функции .

Необходимо указать на ограничение, которое накладывается каскадным включением ЦАП на диапазон изменения масштабного коэффициента . При подаче на цепочку ЦАП кода, близкого к , выходное напряжение -го ЦАП пропорционально . Для эта величина возрастает в геометрической прогрессии и может привести к насыщению операционных усилителей. Поэтому целесообразно устанавливать равным 1 и аппроксимировать функцию исходя из того, что аргумент изменяется от 0 до 1.

Из вышесказанного следует, что для воспроизведения многочлена степени необходимо иметь каскадно включенных ЦАП. Коэффициенты многочлена реализуются подбором резисторов , , а знаки слагаемых устанавливаются с помощью инвертора.

Для того чтобы погрешность, вызванная аппроксимацией (методическая погрешность), была минимальной, необходимо соответствующим образом подобрать коэффициенты многочлена.

Нами рассмотрены три метода вычисления этих коэффициентов.

Наиболее распространенный метод аппроксимации функции – ее разложение в ряд Тейлора. В общем виде это разложение функции в окрестности точки осуществляется по формуле

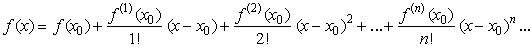
Разложение функции в ряд Тейлора не является единственным. Существует возможность разложить функцию в ряд по обобщенным многочленам, например, по многочленам Лежандра, Чебышева, Якоби, Эрмита или Лагерра. Здесь мы остановимся на многочленах Чебышева, поскольку они дают наилучшее приближение [5,6].

Для нахождения коэффициентов разложения по многочленам Чебышева используем следующие формулы:

;

,

.

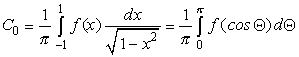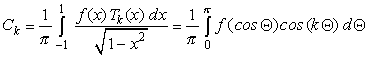Подставив вместо многочленов Чебышева их выражения через переменную , а затем приведя подобные члены, получим искомый многочлен

.

Согласно общим теоремам теории аппроксимации, разложение функции в ряд по многочленам Чебышева дает наилучшее приближение из всех возможных. Необходимо отметить, что разложение функции по многочленам Чебышева возможно только для функций, имеющих непрерывную первую производную на отрезке [–1, 1]. Это условие обеспечивает сходимость ряда к функции . Для большинства элементарных функций это условие выполняется.

Следующий метод основан на теории интерполяции [5]. В этом случае строят многочлен, который в заданных точках , принимает значения , а в остальных точках отрезка , принадлежащего области определения , приближенно представляет функцию с той или иной степенью точности. Для нахождения коэффициентов многочлена составляется система уравнений

, ,

которая легко решается методом Крамера.

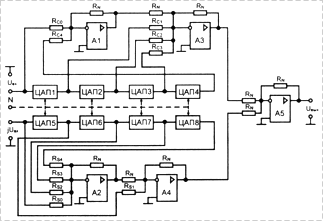
Функциональный ЦАП, использующий степенную аппроксимацию тригонометрических функций, является основой построения широкополосного цифроуправляемого калибратора фазы (рис. 4).

Рис. 4. Широкополосный калибратор фазы
на основе функциональных ЦАП

Выходное напряжение калибратора фазы формируется в соответствии с зависимостью

,

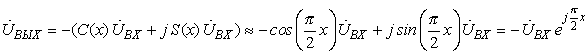где

,

– многочлены, аппроксимирующие функции и . Здесь – относительное значение цифрового кода , подаваемого на входы всех ЦАП, оно изменяется в интервале [0, 1]; – максимальное значение цифрового кода . Это позволяет регулировать угол фазового сдвига в диапазоне от до . Преобразование входного гармонического сигнала по синусоидальному и косинусоидальному законам осуществляется двумя функциональными ЦАП.

Для регулирования угла фазового сдвига в других квадрантах необходимо изменить полярность на выходах одного или двух функциональных ЦАП. Этого можно добиться, добавив инвертор на выход соответствующего функционального ЦАП или выбрав в качестве нелинейного закона преобразования функцию с противоположным знаком.

Степень многочленов и выбирается исходя из требуемой точности, она определяет число используемых в схеме линейных ЦАП. Для упрощения устройства следует стремиться к тому, чтобы уменьшить число каскадно включенных ЦАП без увеличения погрешности.

Методическую погрешность воспроизведения угла фазового сдвига и нестабильность выходных напряжений такого калибратора фазы можно уменьшить, применяя для расчета коэффициентов степенной аппроксимации метод Чебышева или интерполяцию. Методическая погрешность воспроизведения фазового сдвига и нестабильность амплитуды выходного напряжения калибратора фазы определяются по следующим формулам:

;

.

В таблице 1 приведены максимальные значения погрешностей для упомянутых методов в сравнении с методом Тейлора. Здесь – степень многочленов и .

Таблица 1

	Метод Чебышева		Интерполяция		Метод Тейлора
	, °	, %	, °	, %	, °	, %
3	0,07	0,2	0,06	0,2	0,5	1
4	0,009	0,01	0,009	0,01	0,1	0,6
5	0,0006	0,001	0,0006	0,001	0,01	0,06
6	0,0006	0,0003	0,0006	0,0002	0,002	0,002

Анализ данных, приведенных в таблице, показывает, что метод Чебышева и интерполяция дают значительное снижение методических погрешностей в сравнении с разложением в ряд Тейлора. Это обстоятельство позволяет сократить число включенных каскадно ЦАП при заданной погрешности калибратора.

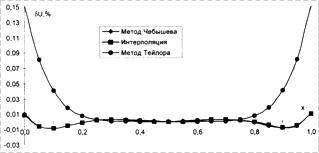
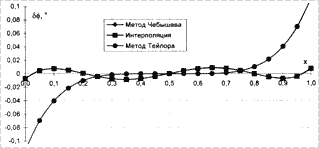
Распределение погрешностей в интервале регулирования фазового сдвига (интервале аппроксимации) для случая показано на рис. 5 и 6. Как видно из графиков, погрешности интерполяции и метода Чебышева практически совпадают.

Рис. 5. Нестабильности выходного напряжения при регулировании фазового сдвига в интервале	Рис. 6. Погрешность воспроизведения фазового сдвига при регулировании в интервале

Рассмотренные функциональные ЦАП и созданные на их основе калибраторы фазы состоят только из интегральных микросхем и резисторов и могут быть изготовлены в виде микросборок. На точность воспроизведения указанных функций заметно влияют отношения сопротивлений резисторов. Интегральное исполнение резисторов позволит снизить погрешности сопротивлений, вызванные температурными колебаниями и обеспечить тем самым более высокие метрологические характеристики.

Список литературы

1. Быстров Ю.А., Великсон Я.М., Вогман В.Д. и др. Электроника: Справочная книга. СПб.: Энергоатомиздат, 1996. 544 с.

2. Федорков Б.Г., Телец В.А. Микросхемы ЦАП и АЦП. М.: Энергоатомиздат, 1990. 320 с.

3. Сапельников В.М., Кравченко С.А., Чмых М.К. Проблемы воспроизведения смещаемых во времени электрических сигналов и их метрологическое обеспечение. Уфа: Изд. Башкирск. гос. ун-та, 2000. 196 с.

4. Сапельников В.М. ЦАП в калибраторах фазы. Уфа: Изд. Башкирск. ун-та, 1997. 152 с.

5. Березин И.С., Жидков Н.П. Методы вычислений. М.: Физматлит., 1959. 464 с.

6. Бронштейн И.Н., Семендяев К.А. Справочник по математике: Для инженеров и учащихся втузов. М.: Наука, 1986. 544 с.

Наверх