УДК 539.219.3:620.186.84:539.373
В.Н.Чувильдеев, д-р физ.-мат. наук, проф., О.Э.Пирожникова, канд. физ.-мат. наук, А.В.Петряев,
Нижегородский государственный университет им. Н.И.Лобачевского
Микромеханизмы зернограничного возврата при отжиге после деформации. Возврат диффузионных свойств границ зерен
![]()
|
Построена модель, позволяющая описывать наблюдаемые экспериментально
изменения энергии активации зернограничной диффузии мелкозернистых
поликристаллических металлов в условиях отжига после деформации. В основе
модели лежат развитые авторами ранее представления теории неравновесных
границ зерен. Показано, что изменения характеристик зернограничной диффузии
мелкозернистых материалов связаны с “уходом” из границ зерен дефектов,
внесенных в границы зерен при предварительной деформации. Получены уравнения,
позволяющие описывать зависимость диффузионных характеристик границ зерен от
времени и температуры отжига, а также структурных параметров материалов. |
Диффузионные свойства
неравновесных границ
Сопоставление с экспериментальными
данными
Описание экспериментальных данных
Описание процедуры сопоставления
Введение
В серии наших работ [1-3] была предложена полуфеноменологическая теория, позволяющая описывать диффузионные свойства равновесных и неравновесных границ зерен. В работе [3] описана модель, позволяющая рассчитывать изменения диффузионных свойств границ зерен при попадании в них решеточных дислокаций. Было показано, что параметры зернограничной диффузии в границах зерен зависят от плотности накапливающихся в границе дислокаций ориентационного несоответствия и продуктов их делокализации.
В работе [4] на основе представлений, развитых в [1-3], были рассчитаны изменения диффузионных параметров границ зерен при их бомбардировке решеточными дислокациями, осуществляющими внутризеренную деформацию в условиях структурной сверхпластичности. Естественным развитием подхода [1-4] является рассмотрение задачи о диффузионном перераспределении (возврате) дефектов в границах зерен при отжиге деформированных поликристаллов и влиянии этого процесса на физико-механические свойства металлов.
В первой части работы рассмотрены процессы возврата диффузионных свойств границ зерен.
Во второй части проанализированы закономерности возврата механических свойств при отжиге деформированных поликристаллов.
Диффузионные свойства неравновесных границ
В работе [1] было показано, что коэффициент зернограничной диффузии ![]() зависит от свободного
объема границ
зависит от свободного
объема границ ![]() а и термодинамических констант материала:
а и термодинамических констант материала:
![]() ;
(1)
;
(1)
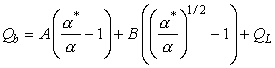 ;
(2)
;
(2)
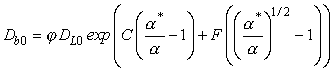 .
(3)
.
(3)
Здесь ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Расшифровка обозначений и характерные числовые значения термодинамических
констант материалов, входящих в соотношения (1) – (3), приведены в
табл. 1.
. Расшифровка обозначений и характерные числовые значения термодинамических
констант материалов, входящих в соотношения (1) – (3), приведены в
табл. 1.
Таблица 1. Значения параметров, используемых при расчетах
|
Параметры |
Обозначения |
Al
2 мкм |
Al
22 мкм |
Сталь A 2,1 мкм |
Сталь B
30 мкм |
|
Параметры границ
раздела |
|||||
|
Энтальпия поверхности
“жидкость-кристалл” ( |
|
1,16 |
0,8 |
||
|
Энтропия поверхности
“жидкость-кристалл” ( |
|
0,92 |
0,92 |
1,4 |
1,35 |
|
Свободная
(поверхностная) энергия “сухих” участков границы ( |
|
1,5 |
1,6 |
||
|
Критический свободный объем границы |
|
0,5 |
0,5 |
||
|
Свободный объем границы |
|
0,38 |
0,273 |
||
|
Диффузионные
параметры |
|||||
|
Энергия активации
самодиффузии в расплаве ( |
|
3,7 |
3,5 |
||
|
Предэкспонента в выражении для коэффициента диффузии в расплаве, см2/с |
|
1,4×10-5 |
8×10-4 |
||
|
Подгоночные параметры |
|||||
|
Числовой множитель в выражении для времени делокализации |
|
20 |
10 |
||
|
Числовой множитель в выражении для времени “ухода” из границы скользящих компонент делокализованных дислокаций |
|
0,15 |
140 |
||
|
Начальная плотность ДОН |
|
0,005 |
0,004 |
0,01 |
0 |
|
Начальная плотность скользящих компонентов делокализованных дислокаций |
|
0,006 |
0,006 |
0 |
0,01 |
|
Кристаллографические
параметры |
|||||
|
Вектор Бюргерса, см |
|
2,86×10-8 |
2,58×10-8 |
||
|
Ширина границы зерна |
|
|
|||
|
Атомный объем, см3 |
|
1,66×10-23 |
1,16×10-23 |
||
|
Термодинамические и
упругие константы |
|||||
|
Удельная теплота плавления |
|
|
|
||
|
Плотность |
|
||||
|
Температура плавления |
|
|
|
||
|
Модуль сдвига, МПа |
|
2,5×104 |
6,0×104 |
||
Относительный свободный объем а определяется по формуле
![]() ,
,
где ![]() – свободный объем границ
зерен в процентах;
– свободный объем границ
зерен в процентах; ![]() – изменение объема при
плавлении [1-3].
– изменение объема при
плавлении [1-3].
При вычислении параметров
самодиффузии в равновесных границах используется значение равновесного свободного
объема а [1-2]. В [2,3] было показано, что при взаимодействии границ зерен с
другими дефектами свободный объем границ изменяется. В частности, при попадании
в границы зерен решеточных дислокаций и делокализации их ядер в границах
возникает избыточный свободный объем ![]() , пропорциональный плотности дислокаций ориентационного несоответствия
, пропорциональный плотности дислокаций ориентационного несоответствия
![]() и плотности скользящих
компонентов делокализованных дислокаций
и плотности скользящих
компонентов делокализованных дислокаций ![]() [3]:
[3]:
![]() ,
(4)
,
(4)
где ![]() – числовой параметр,
равный 0,1 [2,3];
– числовой параметр,
равный 0,1 [2,3]; ![]() – вектор Бюргерса
дислокации ориентационного несоответствия.
– вектор Бюргерса
дислокации ориентационного несоответствия.
При возникновении в границах зерен избыточного свободного объема ![]() их диффузионные характеристики
изменяются. В первом приближении это изменение можно оценить, подставив в (1) –
(3) вместо равновесного значения а величину неравновесного свободного объема
их диффузионные характеристики
изменяются. В первом приближении это изменение можно оценить, подставив в (1) –
(3) вместо равновесного значения а величину неравновесного свободного объема
![]() .
(5)
.
(5)
Выражение для энергии активации зернограничной самодиффузии ![]() (2) в этом случае
примет вид
(2) в этом случае
примет вид
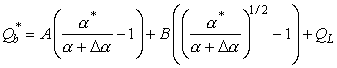 . (6)
. (6)
Величина предэкспоненциального множителя ![]() будет вычисляться по
формуле (обозначения см. табл. 1):
будет вычисляться по
формуле (обозначения см. табл. 1):
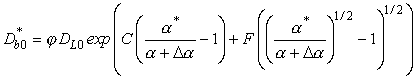 . (7)
. (7)
При малых изменениях свободного объема границ (![]() и
и ![]() ) выражение для
) выражение для ![]() существенно упрощается:
существенно упрощается:
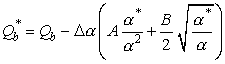 .
(8)
.
(8)
Выражение для ![]() в случае малых
в случае малых ![]() принимает вид
принимает вид
![]() ,
(9)
,
(9)
где ![]() определяется по
формуле
определяется по
формуле
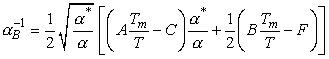 . (10)
. (10)
Как видно из полученных выражений (4) – (9), диффузионные характеристики неравновесных границ зерен существенно зависят от плотности распределенных в границах дефектов.
Кинетика накопления дефектов в границах в случае, когда границы зерен
непрерывно бомбардирует поток решеточных дислокаций, рассмотрена в [3].
Уравнение для плотности дислокаций ориентационного несоответствия при однородном
потоке решеточных дислокаций![]() /имеет вид
/имеет вид
![]() ,
(11)
,
(11)
где ![]() – время размывания
ядер дислокаций ориентационного несоответствия на характерное расстояние
– время размывания
ядер дислокаций ориентационного несоответствия на характерное расстояние ![]() , равное расстоянию между соседними дислокациями
ориентационного несоответствия в границе
, равное расстоянию между соседними дислокациями
ориентационного несоответствия в границе ![]() . Время
. Время ![]() определяется
выражением [3]
определяется
выражением [3]
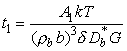 .
(12)
.
(12)
Уравнение, описывающее кинетику накопления скользящих компонентов
делокализованных дислокаций ![]() , может быть представлено в форме
, может быть представлено в форме
![]() .
(13)
.
(13)
Здесь ![]() – характерное время
ухода с границ зерен скользящих компонентов делокализованных дислокаций
– характерное время
ухода с границ зерен скользящих компонентов делокализованных дислокаций ![]() , вычисляемое по формуле [3,5]
, вычисляемое по формуле [3,5]
![]() . (14)
. (14)
В общем случае в границах зерен присутствуют оба типа указанных дефектов и
для описания эволюции дефектной структуры границ зерен необходимо совместное
решение уравнений (11) – (14) с учетом (4) – (10). Сравнивая значения ![]() и
и ![]() при
при ![]() , нетрудно убедиться, что при малых размерах
, нетрудно убедиться, что при малых размерах ![]() зерен в границах
доминируют дислокации ориентационного несоответствия
зерен в границах
доминируют дислокации ориентационного несоответствия ![]() , а при больших
, а при больших ![]() основную роль играют
скользящие компоненты делокализованных дислокаций
основную роль играют
скользящие компоненты делокализованных дислокаций ![]() [3].
[3].
Описание возврата дефектной структуры и диффузионных свойств границ зерен при отжиге после деформации
Развитые выше представления позволяют перейти к описанию изменений параметров границ зерен при отжиге после деформации, т.е. к описанию процессов “возврата” свойств границ зерен к “равновесным” значениям.
Для описания процесса возврата следует воспользоваться уравнениями (11) – (14), приняв, что в условиях отжига поток дислокаций / на границы зерен из объема зерен отсутствует.
В случае ![]() уравнения (11) – (14)
в приближении малых
уравнения (11) – (14)
в приближении малых ![]() (
(![]() ) принимают вид [
) принимают вид [![]() ,
,
![]() ;
;
![]() при
при ![]() ;
(15)
;
(15)
![]() ;
;
![]() при
при ![]() ;
(16)
;
(16)
Решая указанные уравнения с учетом соотношений (1) – (14), нетрудно определить зависимость плотности дефектов и в соответствии с (6) и (7) – параметров зернограничной диффузии от времени и, таким образом, описать процесс возврата диффузионных свойств.
В наиболее распространенном случае, когда плотности различных типов дефектов
в границе сопоставимы (![]() ), система уравнений (15) – (16) не имеет аналитических
решений и ее необходимо решать численно. В случае, когда в границах зерен
доминирует только один тип дефектов [или дислокации ориентационного
несоответствия (
), система уравнений (15) – (16) не имеет аналитических
решений и ее необходимо решать численно. В случае, когда в границах зерен
доминирует только один тип дефектов [или дислокации ориентационного
несоответствия (![]() ) или скользящие компоненты делокализованных дислокаций (
) или скользящие компоненты делокализованных дислокаций (![]() )], уравнения (15) и (16) существенно упрощаются. Однако их
решения имеют простой вид только при
)], уравнения (15) и (16) существенно упрощаются. Однако их
решения имеют простой вид только при ![]() , когда выполняется соотношение
, когда выполняется соотношение ![]() , что соответствует поздним стадиям возврата, когда большая
часть дефектов покинула границу. В этом приближении решения могут быть представлены
в виде
, что соответствует поздним стадиям возврата, когда большая
часть дефектов покинула границу. В этом приближении решения могут быть представлены
в виде
![]() ;
(17)
;
(17)
![]() . (18)
. (18)
Сопоставление с экспериментальными данными
Описание экспериментальных данных
Для сопоставления полученных выражений с экспериментом обратимся к работам [5-7], в которых весьма подробно исследованы процессы возврата диффузионных свойств при отжиге предварительно деформированного высокочистого алюминия [5, 6] и коррозионно-стойкой стали [7].
В указанных работах [5-7] для анализа кинетики возврата в границах зерен используются данные о характере протекания процесса делокализации ядер решеточных дислокаций, внесенных в границы зерен при предварительной пластической деформации. Как известно [8-9], изучение параметров процесса делокализации позволяет определять диффузионные характеристики границ зерен и, в частности, оценивать скорость изменения диффузионных свойств границ при отжиге после деформации. Поскольку указанные экспериментальные работы выполнены в рамках единой методологии, мы подробно опишем результаты работ, посвященных исследованию алюминия [5,6], а в случае сталей [7] ограничимся лишь кратким комментарием.
В работах [5,6] исследованы две группы поликристаллов ![]() и
и ![]() высокочистого алюминия
со средним размером зерна 4 и 22 мкм соответственно, подвергнутых одинаковой
предварительной деформации
высокочистого алюминия
со средним размером зерна 4 и 22 мкм соответственно, подвергнутых одинаковой
предварительной деформации ![]() %. Первичные экспериментальные данные представляют собой
зависимости относительного числа границ зерен (
%. Первичные экспериментальные данные представляют собой
зависимости относительного числа границ зерен (![]() ), содержащих неделокализованные дислокации, от времени
отжига
), содержащих неделокализованные дислокации, от времени
отжига ![]() при разных температурах.
(Для поликристаллов
при разных температурах.
(Для поликристаллов ![]() температуры составляли
293, 343, 373 и 403 К, для поликристаллов
температуры составляли
293, 343, 373 и 403 К, для поликристаллов ![]() – 293 и 373 К.)
– 293 и 373 К.)
Для обработки экспериментальных данных авторы [5,6] использовали формулу
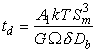 ,
(19)
,
(19)
где ![]() – числовая константа,
зависящая от модельных предположений (в соответствии с [10] величина
– числовая константа,
зависящая от модельных предположений (в соответствии с [10] величина ![]() , в работе [6] принято
, в работе [6] принято ![]() );
); ![]() – ширина ядра
дислокации, при достижении которой дифракционный контраст от дислокации
исчезает при электрономикроскопических наблюдениях. (Для расчетов по формуле
(9) в работах [5,6] используется значение
– ширина ядра
дислокации, при достижении которой дифракционный контраст от дислокации
исчезает при электрономикроскопических наблюдениях. (Для расчетов по формуле
(9) в работах [5,6] используется значение ![]() см.) Анализируя экспериментальные данные, авторы [7,8]
получают, в частности, зависимость значения энергии активации зернограничной
диффузии
см.) Анализируя экспериментальные данные, авторы [7,8]
получают, в частности, зависимость значения энергии активации зернограничной
диффузии ![]() от (
от (![]() ) или от времени выдержки при заданной температуре. Эти
данные приведены в табл. 2.
) или от времени выдержки при заданной температуре. Эти
данные приведены в табл. 2.
Таблица 2. Сопоставление экспериментальных [6] и теоретических значений энергии активации зернограничной диффузии алюминия
|
Размер
зерна, мкм |
Доля
границ зерен, содержащих неделокализованные дислокации |
Энергия
активации, кДж/моль |
|
|
Эксперимент |
Теория |
||
|
4 |
0,2 |
84,6* |
74,0 |
|
0,5 |
64,4 |
64,4 |
|
|
0,8 |
44,3 |
52,7 |
|
|
22 |
0,2 |
49,3 |
52,7 |
|
0,5 |
46,2 |
46,2 |
|
|
0,8 |
42,2 |
41,0 |
|
|
* - данное значение получено путем экстраполяции |
|||
Из проведенного в [5,6] анализа следует, что энергия активации
зернограничной диффузии в поликристаллах ![]() и
и ![]() , имеющих разный размер зерна, при одинаковой степени
возврата существенно отличается. В поликристалле
, имеющих разный размер зерна, при одинаковой степени
возврата существенно отличается. В поликристалле ![]() с большим размером
зерна возврат идет существенно медленнее, чем в мелкозернистом поликристалле
с большим размером
зерна возврат идет существенно медленнее, чем в мелкозернистом поликристалле ![]() . Энергия
активации зернограничной диффузии в
. Энергия
активации зернограничной диффузии в ![]() поликристалле существенно ниже, причем это
отличие заметнее на более поздних стадиях возврата. Действительно, как видно из
табл. 2, при доле не-делокализованных дислокаций в границах, составляющей
20% (на поздних стадиях возврата), энергии активации в кристаллах
поликристалле существенно ниже, причем это
отличие заметнее на более поздних стадиях возврата. Действительно, как видно из
табл. 2, при доле не-делокализованных дислокаций в границах, составляющей
20% (на поздних стадиях возврата), энергии активации в кристаллах ![]() и
и ![]() отличаются на 70% и
равны соответственно 84,6 и 49,3 кДж/моль. При доле 50% они отличаются на
30% и при доле 80% -
на 5%.
отличаются на 70% и
равны соответственно 84,6 и 49,3 кДж/моль. При доле 50% они отличаются на
30% и при доле 80% -
на 5%.
В работе [7] методом, аналогичным описанному выше, исследованы процессы
отжига внесенных в границы зерен дислокаций в коррозионно-стойких сталях А и В,
имеющих различный химический состав (табл. 3) и размер зерен 2,1 и
30 мкм соответственно. В работе получены зависимости ![]() от времени отжига при
различных температурах. Результаты работ [6,7] обобщены в табл. 4.
от времени отжига при
различных температурах. Результаты работ [6,7] обобщены в табл. 4.
Таблица 3. Химический состав (% масс.) коррозионно-стойких сталей [7]
|
Условное
обозначение стали |
C |
Mn |
Si |
P |
S |
Cr |
Ni |
Cu |
Mo |
|
А |
0,12 |
1,23 |
0,47 |
0,028 |
0,008 |
22,3 |
17,0 |
- |
0,28 |
|
В |
0,06 |
0,002 |
0,002 |
0,002 |
0,007 |
19,0 |
18,6 |
0,02 |
0,01 |
Таблица 4. Сопоставление экспериментальных [7] и теоретических значений энергии активации зернограничной диффузии коррозионно-стойких сталей
|
Размер
зерна, мкм / |
Доля
границ зерен, содержащих |
Энергия
активации, кДж/моль |
|
|
Эксперимент |
Теория |
||
|
2,1 / сталь А |
0,2 |
191,2 |
185,7 |
|
0,5 |
190,9 |
163,2 |
|
|
0,8 |
153,4 |
153,4 |
|
|
30 / сталь В |
0,2 |
142,4 |
142,4 |
|
0,5 |
163,8 |
124,1 |
|
|
0,8 |
120,6 |
117,1 |
|
Описание процедуры сопоставления
Обычно при использовании феноменологических моделей предметом дискуссий является число и характер подгоночных параметров, а также приобретает принципиальное значение вопрос о процедуре сопоставления теоретических результатов с экспериментом. В связи этим процедура сопоставления описана далее весьма подробно, шаг за шагом, с указанием всех подгоночных параметров, “возникающих” на каждом “шаге” сопоставления. Числовые значения определяемых параметров для каждого исследованного материала помещены в табл. 1.
Алюминий
1. Найдем значение свободного объема границ зерен ![]() .
.
Используем термодинамические константы алюминия, приведенные
в работе [2], и экспериментальные значения параметров зернограничной диффузии ![]() ,
, ![]() для равновесных границ
зерен, приведенные в работе [6] (см. табл. 1). Подставив указанные
константы в уравнения (1) – (3), получим значение свободного объема
для равновесных границ
зерен, приведенные в работе [6] (см. табл. 1). Подставив указанные
константы в уравнения (1) – (3), получим значение свободного объема ![]() . (Число подгоночных параметров равно 0.)
. (Число подгоночных параметров равно 0.)
2. Найдем значение избыточного свободного объема ![]() в нулевой момент
времени. Энергия активации зернограничной диффузии в начале процесса возврата (
в нулевой момент
времени. Энергия активации зернограничной диффузии в начале процесса возврата (![]() ) в границе, содержащей избыточные дефекты и, соответственно,
избыточный свободный объем
) в границе, содержащей избыточные дефекты и, соответственно,
избыточный свободный объем ![]() , должна быть меньше или равна минимальному
экспериментальному значению энергии активации зернограничной диффузии,
вычисленному в работе [6]:
, должна быть меньше или равна минимальному
экспериментальному значению энергии активации зернограничной диффузии,
вычисленному в работе [6]: ![]() кДж/моль (эта величина соответствует доле неделокализованных
дислокаций 0,8). Используя формулу (6), определим величину
кДж/моль (эта величина соответствует доле неделокализованных
дислокаций 0,8). Используя формулу (6), определим величину ![]() (число подгоночных
параметров равно 0).
(число подгоночных
параметров равно 0).
3. Найдем значение суммарной плотности дефектов в
границах зерен. Подставляя в уравнение (4) значение найденного избыточного
свободного объема ![]() и значение
и значение ![]() [2,3], определим начальную
суммарную плотность ДОН и скользящих компонентов делокализованных дислокаций
[2,3], определим начальную
суммарную плотность ДОН и скользящих компонентов делокализованных дислокаций ![]() (число подгоночных
параметров равно 0).
(число подгоночных
параметров равно 0).
4. Выделим вклады дефектов: дислокаций ориентационного
несоответствия и скользящих компонентов делокализованных дислокаций. Для этого
назначим значение начальной плотности скользящих компонентов делокализованных
дислокаций в нулевой момент времени ![]() (число подгоночных параметров
равно 1).
(число подгоночных параметров
равно 1).
5. В соответствии с кинетическими уравнениями (11) –
(14) вычислим изменения со временем плотности дислокаций ориентационного
несоответствия ![]() и скользящих
компонентов делокализованных дислокаций
и скользящих
компонентов делокализованных дислокаций ![]() при температурах,
указанных в работе [6]. Для этих вычислений необходимо указать числовые
значения параметров
при температурах,
указанных в работе [6]. Для этих вычислений необходимо указать числовые
значения параметров ![]() и
и ![]() , которые выступают здесь подгоночными параметрами. Заметим, что
выбранное здесь значение подгоночного параметра
, которые выступают здесь подгоночными параметрами. Заметим, что
выбранное здесь значение подгоночного параметра ![]() соответствует
значению, приведенному в работе [6]. Значение параметра
соответствует
значению, приведенному в работе [6]. Значение параметра ![]() для алюминия выбрано
равным 0,15. (Заметим, что величина
для алюминия выбрано
равным 0,15. (Заметим, что величина ![]() для сплава Zn – 20% Al равна
3 [4], значение
для сплава Zn – 20% Al равна
3 [4], значение ![]() , приведенное в работе [11], равно 50.) Число подгоночных
параметров равно 2.
, приведенное в работе [11], равно 50.) Число подгоночных
параметров равно 2.
6. Вычислим
на основе (4) – (6) значения энергии активации ![]() на разных стадиях
возврата при заданных температурах. Число подгоночных параметров равно 0.
на разных стадиях
возврата при заданных температурах. Число подгоночных параметров равно 0.
7. Полученные
значения ![]() поместим в табл. 2 и сравним с
экспериментальными данными.
поместим в табл. 2 и сравним с
экспериментальными данными.
Коррозийно-стойкая
сталь
Рассмотрение экспериментальных результатов [7] показывает, что характер возврата в сталях во многом аналогичен характеру процесса возврата в Al и для его анализа можно в основном использовать описанную выше процедуру.
Заметим, однако, что число подгоночных параметров при описании сталей
возрастает, поскольку их термодинамические константы не известны (в отличие от
алюминия, для которого подробные данные приведены в [2]). Используемые при
расчетах термодинамические параметры ![]() ,
, ![]() ,
, ![]() приведены в
табл. 2. Заметим, что эти значения весьма незначительно отличаются от
“средних” значений соответствующих параметров, использовавшихся при численных
расчетах в работах [3,4]. При оценках значений
приведены в
табл. 2. Заметим, что эти значения весьма незначительно отличаются от
“средних” значений соответствующих параметров, использовавшихся при численных
расчетах в работах [3,4]. При оценках значений ![]() предполагается, что
начальное значение энергии активации зернограничной диффузии составляет
предполагается, что
начальное значение энергии активации зернограничной диффузии составляет ![]() кДж/моль (это значение соответствует доле
неделокализованных дислокаций 80%). Значения подгоночных параметров:
кДж/моль (это значение соответствует доле
неделокализованных дислокаций 80%). Значения подгоночных параметров: ![]() (см. [10]),
(см. [10]), ![]() (см. [11]).
(см. [11]).
Сравнение экспериментальных и теоретических значений ![]() для сталей приведено в
табл. 4.
для сталей приведено в
табл. 4.
Анализ результатов
Для алюминия сравнение экспериментальных и теоретических значений энергии
активации показывает весьма хорошее соответствие: расхождение для
поликристаллов ![]() не превышает 6,6%, для
поликристаллов
не превышает 6,6%, для
поликристаллов ![]() превышает 15% (во
втором случае, к сожалению, только две экспериментальные точки, табл. 2).
превышает 15% (во
втором случае, к сожалению, только две экспериментальные точки, табл. 2).
Неплохое соответствие, наблюдаемое в сталях (табл. 4), менее
показательно в силу большого числа подгоночных параметров для алюминия и для
сталей. В рамках изложенной модели находит естественное объяснение существенное
отличие диффузионных параметров мелкозернистого и крупнозернистого поликристаллов.
Как видно из (6) – (9), диффузионные свойства границ зерен зависят от
избыточного свободного объема ![]() . Изменение величины
. Изменение величины ![]() со временем в условиях
отжига после деформации определяется кинетикой диффузионного “ухода” из границ
зерен ДОН и продуктов их делокализации
со временем в условиях
отжига после деформации определяется кинетикой диффузионного “ухода” из границ
зерен ДОН и продуктов их делокализации ![]() . Из (12) и (14) следует, что размер зерна влияет в первую
очередь на кинетику изменения
. Из (12) и (14) следует, что размер зерна влияет в первую
очередь на кинетику изменения ![]() : чем больше
: чем больше ![]() , тем медленнее уходят из границ зерен скользящие компоненты
делокализованных дислокаций.
, тем медленнее уходят из границ зерен скользящие компоненты
делокализованных дислокаций.
Это означает, что даже при одинаковой величине (![]() ), т.е. при одинаковой степени делокализации ДОН, уровень
избыточного свободного объема в границах зерен мелкозернистого и
крупнозернистого материала за счет различия
), т.е. при одинаковой степени делокализации ДОН, уровень
избыточного свободного объема в границах зерен мелкозернистого и
крупнозернистого материала за счет различия ![]() , будет существенно отличаться. Соответственно будут
отличаться и значения энергии активации зернограничной самодиффузии и параметры,
характеризующие интенсивность возврата.
, будет существенно отличаться. Соответственно будут
отличаться и значения энергии активации зернограничной самодиффузии и параметры,
характеризующие интенсивность возврата.
Так, в алюминии, для поликристалла ![]() (имеющего
(имеющего ![]() мкм), чтобы достичь при
мкм), чтобы достичь при ![]() К значений энергии активации, близких к равновесному
К значений энергии активации, близких к равновесному ![]() кДж/моль, требуется
4×106 с,
а в поликристаллах
кДж/моль, требуется
4×106 с,
а в поликристаллах ![]() (
(![]() мкм) для
достижения аналогичного значения
мкм) для
достижения аналогичного значения ![]() при этой температуре
требуется время 2×105 с,
что примерно в 20 раз меньше.
при этой температуре
требуется время 2×105 с,
что примерно в 20 раз меньше.
Для коррозионно-стойких сталей в случае поликристалла с ![]() мкм для достижения значений энергии активации
мкм для достижения значений энергии активации ![]() кДж/моль при
кДж/моль при ![]() К требуется время порядка 2×104 с,
а при
К требуется время порядка 2×104 с,
а при ![]() К – порядка 0,7×104 с. Для поликристалла с
К – порядка 0,7×104 с. Для поликристалла с ![]() мкм для достижения аналогичного значения энергии активации
требуется время порядка 800 и 300 с соответственно.
мкм для достижения аналогичного значения энергии активации
требуется время порядка 800 и 300 с соответственно.
Авторы благодарят за поддержку Международный
научно-технический центр ISTC (грант 1413-00), РФФИ (грант 00-02-16546), а
также Программу “Фундаментальные исследования в высшем образовании” (BRHE) и
Научно-исследовательский и образовательный центр сканирующей зондовой
микроскопии Нижегородского государственного университета
им. Н.И.Лобачевского.
Список литературы
1. Чувильдеев В.Н. Микромеханизмы зернограничной самодиффузии в металлах // ФММ. 1996. Ч. 1-2. Т. 81. № 2. С. 5-14; Т. 81. № 4. С. 52-61.
2. Чувильдеев В.Н. Микромеханизм деформационно-стимулированной зернограничной самодиффузии // ФММ. 1996. Ч. 1-2. Т. 81. № 5. С. 5-13; Т. 81. № 6. С. 5-13.
3. Чувильдеев В.Н., Пирожникова О.Э. Микромеханизм деформационно-стимулированной зернограничной самодиффузии. Ч. 3. Влияние потоков решеточных дислокаций на диффузионные свойства границ зерен // ФММ. 1996. Т. 82. № 1. С. 106-115.
4.
Чувильдеев В.Н., Петряев А.В.
Ускорение зернограничной диффузии при сверхпластичности // ФММ. 2000. Т. 89. № 2. С. 24-28.
5.
Kwiecinski J.,
Wyrzykowski J. Kinetics of recovery on grain boundaries in polycrystalline
aluminium // Acta metall. 1989. V. 37. № 5. P. 1503-1507.
6.
Kwiecinski J.,
Wyrzykowski J. Investigation of grain boundary self-diffusion at low
temperatures in polycrystalline aluminium means of the dislocation spreading
method // Acta metall. 1991. V. 39. № 8. P. 1953-1958.
7.
Swiatnicki W.A.,
Lojkowski W., Grabski M.W. Investigation of grain boundary diffusion
in polycrystals by means of extrinsic grain boundary dislocations spreading
rate // Acta metall. 1986. V. 34. № 4. P. 599-605.
8.
Lojkowski W.,
Grabski M.N. Kinetics of the spreading of extrinsic grain boundary dislocation
of random grain boundaries in metals // Deformation of policrystals. Mechanism
and microstructure: Metal. Mater. Sci. 1981. P. 329-333.
9. Varin R.A. On the relation between temperature and time of the spreading of extrinsic grain boundary // Dislocations and the grain boundary energy in an austenitic steel.-metallkunde. 1982. № 10. P. 654-658.
10. Кужидловски К., Выжиковски Е., Гарбач Г. Анализ моделей процесса делокализации сторонних дислокаций на границах зерен // ФММ. 1988. Т. 65. Вып. 2. С. 385-392.
11. Перевезенцев В.Н. Современные представления о природе структурной сверхпластичности // Вопросы теории дефектов в кристаллах: Сб. науч. трудов. Л., 1987. С. 85-101.
| Наверх |