УДК 621.389:004.2
Г.И.Леонович, д-р техн. наук, Самарский государственный аэрокосмический университет
Согласование энергетических и пространственных параметров оптоэлектронных цифровых преобразователей перемещений
|
Обоснован и изложен принцип согласования энергетических и
пространственных параметров оптоэлектронных цифровых преобразователей
перемещений, позволяющий при проектировании преобразователей исключить ситуации,
когда требуемое отношение сигнал/шум на нагрузке фотоприемника не
обеспечивается величиной отверстия кодирующего элемента и когда площадь
отверстия существенно превышает величину, достаточную для надежной
регистрации оптического сигнала. |
Оптоэлектронные цифровые преобразователи линейных и угловых перемещений (ОЦПП), работающие с некогерентными источниками излучения, нашли широкое применение при решении задач контроля и управления микротурбинами, измерения перемещения исполнительных устройств в мини- и микроробототехнических системах и в других объектах микросистемной техники.
ОЦПП по принципу квантования преобразуемой величины можно разделить на две основные группы [1,2,5,7].
Первая группа – одноотсчетные преобразователи – содержит кодирующий элемент
(КЭ), который преобразует перемещение 
непосредственно в
дискретный оптический или электрический сигнал. Цифровой эквивалент перемещения
получается либо методом реверсивного счета единичных приращений, либо методом
считывания.
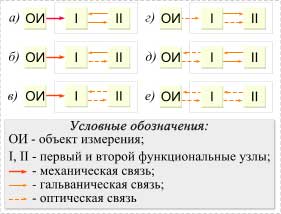
Вторая группа (рис. 1) – двухотсчетные ОЦПП – содержит помимо одноотсчетного ОЦПП второй функциональный узел – вторичный преобразователь, в котором цифровому преобразованию подвергается аналоговый сигнал, пропорциональный смещению в дискретных участках, на которые разбит весь диапазон перемещения. Дискреты задаются КЭ или модуляторами светового потока типа муаровых, матричных, нониусных и других шкал. Двухотсчетные ОЦПП строятся, как правило, по следующему принципу: первый отсчет – накапливающий или считывающий, второй – с интерполяцией амплитуды или пространственной фазы промежуточных сигналов. Связь ОЦПП с объектом измерения может быть механической или оптической; связь между функциональными узлами, формирующими первый и второй отсчеты, – оптической или гальванической.
|
|
|
Рис. 1. Варианты разделения
функциональных узлов |
Информационная емкость ОЦПП определяется как максимально возможное
количество информации, получаемое при единичном отсчете по отдельной &-й
кодовой комбинации, где 
; 
; 
– число разрядов ОЦПП
[5]. В двухотсчетных преобразователях код 
перемещения получается
путем суммирования кодов первого 
и второго 
отсчетов (
) по 
-й кодовой комбинации. При диапазоне 
изменения перемещения истинное значение
измеряемого параметра должно находиться внутри одного из интервалов 
, где 
– шаг квантования. В
реальных ОЦПП координаты границ квантов не совпадают с расчетными на величину 
, которая называется погрешностью воспроизведения уровня
квантования. Текущие значения этой погрешности при -й кодовой комбинации обозначаются 
.
Количество информации в -й кодовой комбинации с учетом этой погрешности оценивается
величиной [5]:
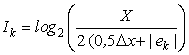. (1)
Погрешности формируются из большого числа доминирующих и слабо зависимых величин, которые по функциональным признакам можно представить суммой групп независимых слагаемых. В первую группу входят инструментальные погрешности, параметры которых определяются конструкцией ОЦПП, принятыми технологиями изготовления считывающей системы и КЭ, нанесения на КЭ кодового поля, изготовления комплектующих деталей и элементов, их сборки в единую конструкцию с последующей юстировкой и настройкой. Вторая группа представляет собой совокупность дополнительных погрешностей воспроизведения квантованных уровней, порождаемых воздействием внешних дестабилизирующих факторов в процессе функционирования ОЦПП, а также естественным износом и старением материалов.
Вместе с тем, точность ОЦПП определяется энергетическими показателями
информационно-энергетических каналов (ИЭК), каждый из которых включает 
-й или общий для всех фотоприемников источник излучения,
среду распространения света, оптическую систему, диафрагмы, 
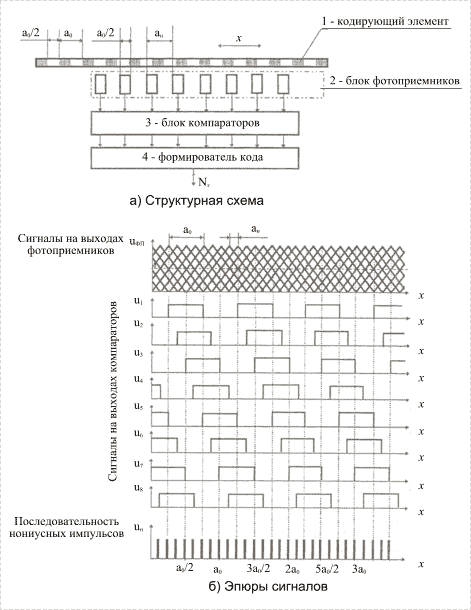
-е профилированное отверстие (зону прозрачности) КЭ и -й фотоприемник. На рис. 2 в качестве примера
представлена структурная схема (а) и эпюры сигналов (б) нониусного ОЦПП [3].
Здесь при общем протяженном источнике излучения код формируется
реверсивным счетом числа отверстий, перемещающихся относительно других по
правилу нониусной шкалы. Такой тип интерполяции является пространственно-фазовым.
|
|
|
Рис. 2. Двухотсчетный нониусный ОЦПП |
Энергетический динамический диапазон ИЭК определяется формулой [7]
, (2)
где 
и 
– максимальное и
минимальное значения мощности информационного сигнала при прохождении светового
потока от -го или общего излучателя через -е отверстие КЭ -му фотоприемнику.
Для упрощения анализа в дальнейшем будем считать, что 
, т.е. исследуется сигнал на выходе одного фотоприемника.
Тогда текущее количество информации в ИЭК при 
-й кодовой комбинации, пространственно соответствующей 
-му отверстию КЭ без учета информационной емкости самого КЭ,
можно в виде формулы
,
(3)
где 
, 
– текущее значение
мощности сигнала при -й кодовой комбинации; 
– минимальное значение
мощности сигнала, различимого на фоне помех.
Уравнение (3) позволяет сформулировать требования, предъявляемые к энергетическим характеристикам ОЦПП. Для одноотсчетного ОЦПП условия, обеспечивающие согласование пространственных и энергетических параметров, записываются в виде неравенства
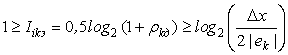, (4)
а для двухотсчетного – в виде неравенства
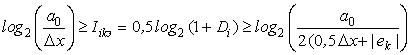, (5)
где 
– шаг нанесения
отверстия младшей разрядной дорожки КЭ (в одноотсчетном ОЦПП 
); 
– допустимое отношение
сигнал/шум, обеспечивающее устойчивое выделение сигнала из смеси сигнала и шума
выбранным методом; 
– допустимая мощность
сигнала; 
– мощность шума на
выходе регистратора при 
-й кодовой комбинации.
Левые части неравенств (4) и (5) обозначают пространственную границу точности,
выше которой поднимать энергетическую информационную способность
нецелесообразно, так как рост энергетических показателей не ведет к улучшению
точности из-за погрешностей 
. Правые части неравенств показывают энергетическую границу,
ниже которой происходит полная потеря информации в одноотсчетном
преобразователе и потеря от одного до нескольких разрядов информации – в
двухотсчетном.
Одно- и двухотсчетный ОЦПП можно представить как совокупность из 
одноканальных
модуляторов, по одному на каждое отверстие КЭ. Тогда по значениям 
и 
, подставляемым в уравнение (4) и (5), можно сформулировать
условия энергетического обеспечения достоверности всех 
кодовых комбинаций.
Для одноотсчетного ОЦПП можно считать, что источник излучения создает одинаковую освещенность по всей площади отверстия КЭ, а для двухотсчетного – по площади части отверстия, пропорциональной цене младшего разряда кода перемещения. Тогда максимальное значение амплитуды потока, соответствующее младшему разряду кода для одно- и двухотсчетного преобразователей, может быть определено по формуле [2]
, (6)
где 
– амплитуда
освещенности, создаваемой источником излучения на чувствительной поверхности
фотоприемника (ФП) при единичном значении функции пропускания оптического
канала; 
и 
– интегральные
коэффициенты пропускания оптической среды (вместе с оптической системой) и
прозрачных частей КЭ для потока излучения полезного сигнала соответственно; 
– площадь единичного
отверстия на младшей разрядной дорожке КЭ; 
– число разрядов во
втором отчете (для одноотсчетного преобразователя 
).
Суммарную спектральную
плотность мощности помех можно представить в виде суммы слагаемых, по-разному
зависящих от параметров оптической системы и электронного тракта. Внутренние
шумы фотоприемника – дробовые, токовые, тепловые и
генерационно-рекомбинационные шумы (в том числе шумы типа 
) – имеют спектральные плотности мощности, которые в общем
виде определяются по следующим формулам [1,4]:
; 
; 
, 
,
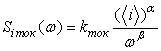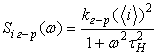где 
– среднее значение
силы тока, протекающего через ФП; 
– заряд электрона; 
– постоянная
Больцмана; 
– абсолютная
температура ФП; 
– среднее время жизни
носителя заряда в полупроводниковых ФП; 
– внутреннее
сопротивление инфракрасного ФП; 
– частота колебаний; 
, 
, 
, 
, 
– коэффициенты,
получаемые эмпирическим путем.
При работе фотоприемника в фотодиодном режиме можно считать, что 
, 
, 
[1]. Шумы типа 
резко ослабляются введением
модуляции светового потока по каналу питания излучателя.
Дополнительные внутренние
шумы генерируются активными сопротивлениями нагрузочной цепи 
и в элементах
усилителя фототока 
. В точке приложения на входе в усилитель суммарный шум можно
представить спектральной плотностью мощности [4]:
,
где 
– - частотная
передаточная функция усилителя фототока.
Суммарная спектральная плотность мощности помех описывается выражением
,
(7)
где 
– спектральная
плотность фотонных шумов.
В общем случае отношение сигнал/шум определяется по формуле [4]
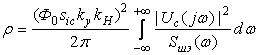, (8)
где 
– спектр полезного
сигнала; 
, 
– коэффициенты
усиления и нагрузки фотоприемного усилителя соответственно; 
– интегральная чувствительность
фотодиода.
Если значение отношения вычислено по заданному отношению сигнал/шум, то в
правой части уравнения (8) регулируемыми или выбираемыми параметрами являются
значения 
, 
, 
и 
. Нахождение этих параметров осуществляется численным
способом в форме решения оптимизационной задачи. Дополнительно накладываемые
условия – ограничение габаритных размеров, массы, энергоемкости и др.
В качестве примера можно
привести методику расчета высоты отверстий младшей разрядной дорожки КЭ в
одноотсчетном ОЦПП. Для упрощения расчетов будем считать, что суммарный шум
состоит из дробовых шумов ФП и тепловых шумов на нагрузочном сопротивлении.
Максимальная скорость 
перемещения отверстия КЭ определяет период и
время съема информации в одной выборке 
-й кодовой
комбинации соответственно как 
(
– число выборок) и 
. Максимальная амплитуда силы тока в процессе отсчета на
нагрузочном сопротивлении, соответствующая совпадению геометрических проекций
отверстий КЭ и диафрагмы, определяется выражением
.
Среднее значение амплитуды тока при перемещении отверстия через линию
считывания в пределах диапазона 
, равно 
.
Считая все параметры, кроме 
, известными, запишем:
,
где 
.
С учетом дробового и теплового шумов спектральная плотность мощности флуктуации тока в нагрузочном сопротивлении равна:
.
(9)
Подставляя значения параметров сигнала и помехи из (9) в формулу (8), получим:
, (10)
где 
– спектр
последовательности из прямоугольных
импульсов единичной амплитуды длительностью 
и периодом следования 
. В соответствии с теоремой Парсеваля при периоде наблюдения 
[6]:
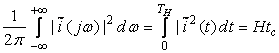. (11)
Подставив (11) в (10), получим:
.
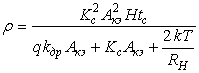(12)
Будем считать, что величина 
. Зададимся
величиной информационной емкости КЭ 
. Диапазон
линейного перемещения 
мм, период
нанесения отверстий КЭ 
мкм. Будем также считать, что за период считывания, равный 
мкс, проводится три отсчета информации (
), длительность импульсов 
мкс. Исходя из принятых стандартных параметров осветителей и
оптической среды (
мкВт; 
, 
; 
мкА/мкВт; 
), получим значение 
.
Решая уравнение (12) относительно неизвестного 
определим значение
площади отверстия КЭ:
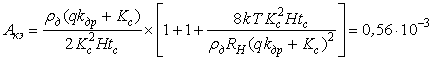[мм2]. (13)
При известных значениях периода нанесения и ширины отверстий КЭ получается,
что высота одного отверстия (нижняя граница), обеспечивающего по энергетике
оптического сигнала заданную пространственно-позиционную точность, равна 
мм.
Для двухотсчетного преобразователя вместо порогового значения отношения
сигнал/шум в (13) подставляется величина энергетического диапазона 
, а варьируемой (искомой) величиной при заданных 
и фиксированной высоте
отверстий выбирается
значение периода 
нанесения меток на КЭ.
Рассмотренная методика согласования энергетических и пространственных параметров может применяться для всех типов оптоэлектронных датчиков, построенных на принципе амплитудной модуляции некогерентного светового потока.
Список литературы
1. Аш Ж. и др. Датчики измерительных систем: В двух книгах. Кн. 1 // Пер. с франц. М.: Мир, 1992. 480 с.
2. Якушенков Ю.Г. Теория и расчет оптико-электронных приборов. М.: Советское радио, 1980. 380 с.
3. Конюхов Н.Е. Оптоэлектронные измерительные преобразователи. Л.: Энергия, 1977. 160 с.
4. Порфирьев Л.Ф. Основы теории преобразования сигналов в оптико-электронных системах. Л.: Машиностроение, 1989. 387 с.
5. Домрачев В.Г., Скрипник А.Б. Определение количества информации на выходе цифрового преобразователя угла // Измерительная техника. 1995. № 1. С. 14-15.
6. Вайнштейн Л.А., Зубаков В.Д. Выделение сигналов на фоне случайных помех. М.: Сов. радио, 1960. 448 с.
7. Леонович Г.И. Оптоэлектронные цифровые датчики перемещений для жестких условий эксплуатации. – Самара: Изд-во СГАУ, 1998. 264 с.
| Наверх |