УДК 621.3.049.77.001.2
Б.Г.Коноплев, д-р техн. наук, проф., И.Е.Лысенко, Таганрогский государственный радиотехнический университет
Моделирование микрозеркала с электростатической активацией
![]()
|
Разработано интегральное микрозеркало с электростатической
активацией, изготавливаемое по технологии поверхностной микрообработки.
Предложена модель для расчета поворотного узла микрозеркала. |
Интегральные микрозеркала с электростатической активацией находят широкое применение в миниатюрных робототехнических системах (в качестве оптических ключей) и системах анализа и обработки изображений (для отклонения лазерного луча или светового потока) [1-4].
Описанные в литературе [4,5] микрозеркала с электростатической активацией, выполненные на основе поликремния и алюминия, имеют ряд существенных недостатков. Для микрозеркал, выполненных из поликремния, используется полезная площадь подложки под размещение креплений структурных слоев микрозеркала [5]. Применение в качестве структурного материала для микрозеркал алюминия не позволяет изготовлять данный тип микрозеркал в одном технологическом процессе с другими элементами микрооптикоэлектромеханических систем, так как в технологии поверхностной микрообработки нанесение металла проводится на последнем этапе процесса [6].
В настоящей работе приведена конструкция интегрального микрозеркала с электростатической активацией на основе поликремния, изготовляемого по технологии поверхностной микрообработки. В разработанной конструкции крепление микрозеркала располагается под структурными слоями, т. е. не требуется дополнительной площади подложки (рис. 1).
|
|
|
Рис. 1. Структура интегрального микрозеркала |
При подаче напряжения на один из отклоняющих электродов между ним и структурой микрозеркала возникает электростатическая сила, которая притягивает микрозеркало к отклоняющему электроду. Когда отклоняющее напряжение отключается, микрозеркало под действием силы упругости возвращается в исходное положение.
Электростатическая сила ![]() , возникающая между отклоняющим электродом и структурой
микрозеркала, определяется следующим выражением [7]:
, возникающая между отклоняющим электродом и структурой
микрозеркала, определяется следующим выражением [7]:
![]() , (1)
, (1)
где ![]() – относительная
диэлектрическая проницаемость воздушного зазора;
– относительная
диэлектрическая проницаемость воздушного зазора; ![]() – электрическая
постоянная;
– электрическая
постоянная; ![]() ,
, ![]() – длина и ширина части
отклоняющего электрода, расположенной под структурой микрозеркала;
– длина и ширина части
отклоняющего электрода, расположенной под структурой микрозеркала; ![]() – расстояние между
отклоняющим электродом и структурой микрозеркала;
– расстояние между
отклоняющим электродом и структурой микрозеркала; ![]() – отклоняющее
напряжение; индекс
– отклоняющее
напряжение; индекс ![]() принимает значения 1,
2 для соответствующих отклоняющих электродов. Так, электростатическая сила
принимает значения 1,
2 для соответствующих отклоняющих электродов. Так, электростатическая сила ![]() для электрода 1 будет
выражаться через длину
для электрода 1 будет
выражаться через длину ![]() и ширину
и ширину ![]() части электрода 1,
расположенной под структурой микрозеркала, и напряжение отклонения
части электрода 1,
расположенной под структурой микрозеркала, и напряжение отклонения ![]() . Аналогичным будет выражение для силы
. Аналогичным будет выражение для силы ![]() электрода 2
электрода 2
Под действием силы ![]() структура микрозеркала
притягивается к отклоняющему электроду. По закону Гука силе
структура микрозеркала
притягивается к отклоняющему электроду. По закону Гука силе ![]() , действующей на микрозеркало, будет противодействовать сила
упругости
, действующей на микрозеркало, будет противодействовать сила
упругости ![]() , равная по модулю электростатической силе и противоположная
по направлению [7]:
, равная по модулю электростатической силе и противоположная
по направлению [7]:
![]() , (2)
, (2)
где ![]() – жесткость пластин
крепления;
– жесткость пластин
крепления; ![]() – перемещение,
совершаемое пластинами крепления под действием электростатической силы
– перемещение,
совершаемое пластинами крепления под действием электростатической силы ![]() .
.
Жесткость пластин крепления определяется следующим выражением [7]:
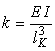 ,
,
где ![]() – модуль Юнга;
– модуль Юнга; ![]() - момент инерции
трапециевидного сечения пластин крепления;
- момент инерции
трапециевидного сечения пластин крепления; ![]() – ширина поверхности
первого структурного слоя;
– ширина поверхности
первого структурного слоя; ![]() – толщина первого
структурного слоя;
– толщина первого
структурного слоя; ![]() – угол, получаемый в
результате анизотропного травления структурных слоев;
– угол, получаемый в
результате анизотропного травления структурных слоев; ![]() – длина пластин
крепления.
– длина пластин
крепления.
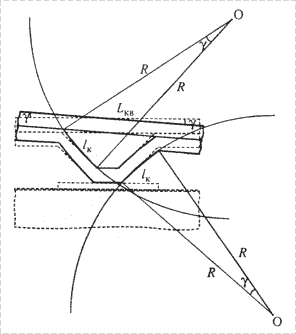
Под действием
электростатической силы ![]() пластины крепления
будут изгибаться по окружностям с центром в точке О, радиусом изгиба
пластины крепления
будут изгибаться по окружностям с центром в точке О, радиусом изгиба ![]() и углом изгиба
и углом изгиба ![]() (рис. 2). Для
определения малых значений угла изгиба у (менее 10°) используется следующее
выражение:
(рис. 2). Для
определения малых значений угла изгиба у (менее 10°) используется следующее
выражение:
![]() .
(3)
.
(3)
|
|
|
Рис. 2. Модель движения |
Как показали результаты
моделирования при расчете электростатической силы ![]() , необходимо учитывать отклонение
, необходимо учитывать отклонение ![]() структуры
микрозеркала, а перемещением пластин крепления можно пренебречь, так как оно
является незначительным по сравнению с размерами микрозеркала. Тогда из (1) –
(3) получим выражение для определения угла изгиба:
структуры
микрозеркала, а перемещением пластин крепления можно пренебречь, так как оно
является незначительным по сравнению с размерами микрозеркала. Тогда из (1) –
(3) получим выражение для определения угла изгиба:
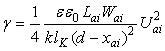 ,
(4)
,
(4)
где ![]() - отклонение,
совершаемое структурой микрозеркала в сторону отклоняющего электрода
- отклонение,
совершаемое структурой микрозеркала в сторону отклоняющего электрода
![]() , (5)
, (5)
где ![]() – длина основания
крепления структуры микрозеркала; 0 – угол травления жертвенного слоя.
– длина основания
крепления структуры микрозеркала; 0 – угол травления жертвенного слоя.
Из (5) при ![]() получим выражение для
определения максимального угла поворота структуры микрозеркала
получим выражение для
определения максимального угла поворота структуры микрозеркала
![]() .
(6)
.
(6)
Из (4) можно получить выражение для напряжения замыкания, при котором произойдет контакт структуры микрозеркала и отклоняющего электрода:
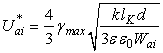 .
(7)
.
(7)
Если ![]() , то
, то ![]() ;
; ![]() ;
; ![]() . Тогда выражение (4) – (7) принимают следующий вид:
. Тогда выражение (4) – (7) принимают следующий вид:
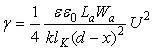 ;
;
![]() ;
;
![]() ;
;
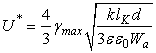 .
.
Быстродействие (максимальная частота вынужденных колебаний) микрозеркала ограничивается частотой собственных упругих колебаний микрозеркала. Согласно закону Гука вызванная деформацией сила пропорциональна значению деформации. Частота упругих гармонических колебаний структуры микрозеркала определяется следующим выражением [7]:
![]() , (8)
, (8)
где ![]() – собственная частота
колебаний микрозеркала;
– собственная частота
колебаний микрозеркала; ![]() – масса колебательной
системы микрозеркала;
– масса колебательной
системы микрозеркала; ![]() – коэффициент
затухания.
– коэффициент
затухания.
Из (8) с учетом геометрии структуры микрозеркала получим выражение
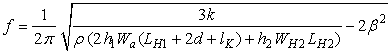 ,
,
где ![]() – плотность поликремния;
– плотность поликремния; ![]() – толщина второго структурного слоя;
– толщина второго структурного слоя; ![]() – длина основания
первого структурного слоя;
– длина основания
первого структурного слоя; ![]() – длина поверхности
крепления;
– длина поверхности
крепления; ![]() – длина основания
второго структурного слоя;
– длина основания
второго структурного слоя; ![]() – технологическая норма изготовления;
– технологическая норма изготовления; ![]() – ширина основания
второго структурного слоя.
– ширина основания
второго структурного слоя.
С использованием предложенной модели проведено моделирование характеристик микрозеркала. Некоторые результаты моделирования представлены на рис. 3-5.
|
|
|
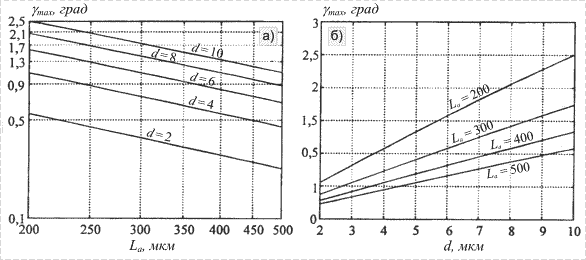
Рис.3. Зависимости максимального угла поворота структуры
микрозеркала |
|
|
|
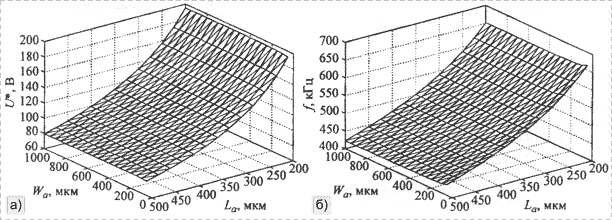
Рис. 4. Зависимости напряжения замыкания |
|
|
|
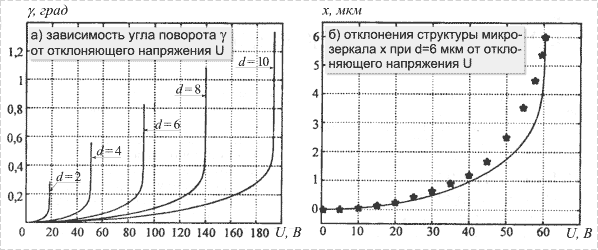
Рис. 5 |
Срез зависимости угла поворота у от отклоняющего напряжения ![]() (рис. 5,а) соответствует режиму замыкания
структуры микрозеркала и отклоняющего электрода. На рис. 5,б наряду с
результатами моделирования отклонения структуры микрозеркала х с использованием
предложенной модели приведены результаты численного моделирования [3] (пакет
программ ANSYS [8]).
Показано, что погрешность моделирования по сравнению с численными методами не
превышает 10%.
(рис. 5,а) соответствует режиму замыкания
структуры микрозеркала и отклоняющего электрода. На рис. 5,б наряду с
результатами моделирования отклонения структуры микрозеркала х с использованием
предложенной модели приведены результаты численного моделирования [3] (пакет
программ ANSYS [8]).
Показано, что погрешность моделирования по сравнению с численными методами не
превышает 10%.
Работа выполнена при финансовой
поддержке Министерства образования РФ (проект 208.06.01.004 в рамках
раздела “Микро- и наносистемная техника “ научно-технической подпрограммы
“Электроника” программы “Научные исследования высшей школы по приоритетным
направлениям науки и техники”).
Список литературы
1.
Бочаров Л.Ю., Эпинатьев И. Д.
Состояние и перспективы развития подводных мини- и микроробототехнических
систем зарубежом // Микросистемная техника. 2000. № 4. С. 39.
2.
Bulk-etched
surface micromachined and flip chip integrated micromirror array for infrared
applications / Tuantranont A. Liew L.-A., Bright V.M. et al.// URL:
http://mems.colorado. edu.
3.
Jung K.,
Lee J., Choi B. Numerical analyses of the micromirror for projection
TV using FEM // Microsystem Technologies. 2001. № 7. P. 75-79.
4.
Fujita H.,
Toshiyoshi H. Optical MEMS // IEICE Trans. Electron. 2000. Vol. E83-C,
№ 9. P. 1427-1434.
5.
Michalicek M.A.
Introduction to micromechanical systems // URL: http://mems.colorado.edu.
6. Koester D.A., Mahadevan R., Hardy В., Markus K.W. MUMPs design handbook // Revision 5.0. URL: http: // www.memsrus.com.
7.
Кухлинг Х. Справочник по физике: Пер. с нем. М.: Мир, 1982. 520 с.
8.
ANSYS
Manual. ANSYS Inc. URL: http://www.ansys.com.
| Наверх |