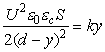УДК 621.3.049.77.002.5
Д.И.Биленко, канд. физ.-мат. наук,
М.Е.Плякин, Д.В.Терин, Л.В.Хохлова, НИИ механики и физики,
Саратовский государственный университет им. Н.Г.Чернышевского
МИКРО- И НАНОЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИ СТРУКТУР С ФАЗОВЫМИ ПЕРЕХОДАМИ
|
Установлена возможность создания МЭМС-аналогов
сред с фазовыми переходами металл-полупроводник или металл-диэлектрик на
основе периодических структур и структур с композитом, свойства которых могут
обратимо изменяться в зависимости от амплитуды и (или) частоты поданного
управляющего напряжения или механического воздействия на управляющие
элементы, и исследованы резонансные явления в этих структурах. |
Регулярная электромеханическая структура
– аналог среды с самораспространяющимся фазовым переходом
Микроэлектромеханическая система
на основе композитной среды
Резонансные явления в
МЭМС-аналогах сред с ФП
Введение
Актуальной задачей является создание сред, обратимо и управляемо-изменяющих ряд своих свойств при управлении внешними сигнальными воздействиями. Такие среды, получившие название разумных, или интеллектуальных (SMART – Self-Monitoring, Analysis and Reporting Technology), перспективны для новых классов устройств и систем в различных областях. В основе действия традиционных современных электронных устройств лежит управляемое перемещение электронных потоков в вакууме или твердом теле. При этом фазовое состояние компонентов, как и их пространственное расположение, неизменны. Такая технология встречается с рядом принципиальных трудностей, в частности, при создании: микро- и наносистем, объединяющих получение информации с ее обработкой и реализацией действий; искусственных нейронов и нейронных сетей; устройств большой площади для сверхширокополосного преобразования и управления излучением; возобновляемых источников энергии.
К перспективным направлениям решения указанных задач относят использование микро- и наноэлектромеханических систем (МЭМС и НЭМС) [1] и фазовых переходов металл-полупроводник и металл-диэлектрик (ФПМП и ФПМД) [2]. Интенсивное развитие МЭМС и НЭМС подтвердило их эффективность и в то же время выявило присущие им ограничения и необходимость учета ранее не рассматривавшихся явлений, в частности, силы Казимира и сил Ван дер Ваальса. Использование известных материалов с ФПМП ограничивается рядом факторов – инерционностью, малым рабочим температурным интервалом, энергоемкостью. Статья посвящена изучению возможностей создания микро- и наноэлектромеханических систем – аналогов структур с фазовым переходом (ФП). Базовым явлением служит перемещение элементов структуры под действием сил упругости и электростатического взаимодействия, силы Казимира и сил Ван дер Ваальса. Эти перемещения приводят к изменению макропараметров, характерных для ФП (проводимости, комплексной диэлектрической проницаемости, оптических, теплофизических и механических характеристик). Если размеры базовых элементов или ячеек существенно меньше характеристических длин, такие системы могут рассматриваться как гомогенные. Например, по отношению к излучениям с длинами волн, много большими размеров базовых элементов или ячеек, такая среда квазиоднородна. Это позволяет рассматривать такие структуры, как композиты и описывать их свойства макропараметрами, используемыми по отношению к однородным средам. Рассмотрение проведено для двух типов структур – периодической с регулярным расположением элементов и структуры со случайным их распределением.
Регулярная электромеханическая структура – аналог среды с самораспространяющимся фазовым переходом
|
|
|
Рис. 1.
Микроэлектромеханическая |
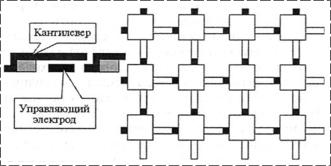
Рассматривается предложенная структура (рис. 1), в которой реализуется последовательное переключение элементов из одного состояния в другое и осуществляется самораспространение переключенного состояния вдоль структуры и переход ее в новое состояние (принцип домино).
Базовым элементом структуры является ячейка, содержащая подвижные элементы – кантилеверы, замыкающиеся на электроды основания при создании достаточной разности потенциалов между кантилевером и управляющим электродом. Массив ячеек, каждая из которых имеет два кантилевера и две контактные площадки, образуют плоскость, свойствами которой можно управлять, варьируя потенциал на управляющих электродах входных ячеек. При подаче на одну из ячеек входного сигнала, больше порогового, происходит последовательное переключение всех ячеек. Входные ячейки могут располагаться как на периферии, так и внутри структуры и могут быть специализированными для начального переключения при механическом, оптическом, тепловом воздействии или изменении переключающего напряжения в результате адсорбции. В замкнутом положении ключи будут оставаться до тех пор, пока напряжение на входе не упадет ниже обратного порогового напряжения; различие прямого и обратного пороговых напряжений (гистерезис) обеспечивает память воздействия. Варьируя tc – отношение толщины тонкого диэлектрического слоя, нанесенного на управляющий электрод dc, к начальному зазору между подвижным и управляющим электродами d, можно управлять шириной петли гистерезиса в широких пределах. Размах петли гистерезиса характеризуется величиной R=Uoff/Uon, где Uon и Uoff – напряжения, вызывающие прямой и обратный переходы. Показано, что:
,
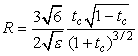где 
‑
диэлектрическая проницаемость диэлектрического слоя.
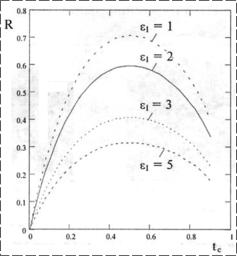
Возможности создания заданной ширины петли гистерезиса при использовании различных диэлектриков иллюстрируются рис. 2.
|
|
|
Рис. 2. Зависимость
отношения напряжения |
Таким образом, изменяя напряжение на управляющем электроде в одной ячейке, можно вызвать последовательное переключение всех ячеек и переход всей структуры из одного состояния, в котором она была подобна диэлектрической среде, в проводящую среду. При этом изменяются электрофизические, электродинамические, оптические, теплофизические и механические свойства среды. Осуществляемый таким образом переход из одного состояния в другое – аналог фазового перехода, в частности, фазового перехода металл – полупроводник. Следует особо отметить, что в отличие от ФПМП энергия на поддержание любого из состояний не расходуется. Основные характеристики предложенного аналога сопоставлялись с параметрами наиболее широко исследованного и нашедшего ряд применений в электронике ФПМП в VO2 [2]. Рассчитывались действующие напряжения, времена, характеристики гистерезиса и энергии переключения одной ячейки и управляемой плоскости.
Поскольку начальное расстояние d между
кантилевером и основанием и перемещение кантилевера у изменяются от единиц
микрометров до долей нанометра, действующая сила записывалась с учетом сил
электростатического притяжения и упругости 
, 
силы Казимира 
[3,4], сил
Ван дер Вальса 
и трения 
(здесь U
Рассматривались системы с сосредоточенным и распределенным взаимодействием. Решались динамическая задача, позволившая изучить колебания в ячейке и времена ее переключения, и статическая задача для установления зависимостей пороговых напряжений прямого и обратного переключений системы и энергии переключения от ее конструктивных параметров и свойств материалов. Базовыми являлись дифференциальные уравнения, связывающие смещение (прогиб) кантилевера с конструктивными параметрами и приложенным напряжением:
;
,
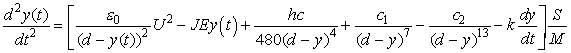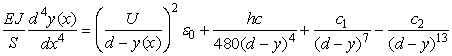здесь t – время; E и J – модуль Юнга и момент инерции подвижного элемента; M – масса.
Установлено, что в ячейках с d>100 нм определяющими динамику ячеек и процессы срыва (переключения) являются силы Кулона и упругости, силы Казимира становятся существенными при d <100 нм, а силы Ван дер Ваальса – при d<20 нм.
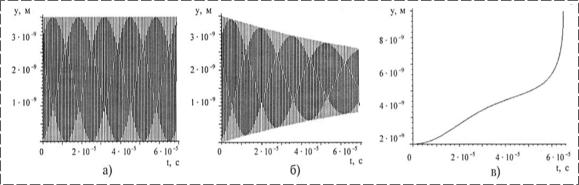
Обнаружено, что силы Казимира и упругости даже в отсутствие внешнего напряжения при соответствующих условиях устанавливают в ячейке колебания, энергия которых обеспечивается энергией физического вакуума, а скорость изменения амплитуды – параметрами ячейки и силами трения (рис. 3, а,б). Разность потенциалов на уровне 0,1 мВ может вызвать переключение системы из высокоомного разомкнутого в замкнутое состояние (рис. 3, в).
|
|
|
Рис. 3. Колебания, обусловленные силой Казимира и силой
упругости |
Реализуемые конструктивные параметры ячейки при d ≈10÷1000 нм позволяют создавать управляемые среды, которые по основным параметрам сопоставимы или значительно превосходят среды на основе ФПМП в VO2. Это иллюстрируется представленными в таблице результатами, полученными для рассматриваемой структуры, специально не оптимизированной.
В таблице представлены данные для структуры, изготавливаемой на основе обычной микроэлектронной технологии с топологической нормой ~1 мкм. Использование современных методов самоформирования наноструктур, подобных описанным в [5], позволит, как показали расчеты, снизить энергию и время переключения на 5-6 порядков.
Сопоставление параметров ФПМП в VO2 и параметров ячейки и плоскости
|
Параметр |
ФПМП в VO2 |
Одна ячейка |
Управляемая плоскость |
|
Время полного цикла
переключения |
Единицы секунд |
3 мкс |
1,2 мс |
|
Энергия переключения |
>10-3 Дж/см2 |
0,12·10-12 Дж |
0,05·10-8 Дж/см2 |
|
Предельная рабочая
температура |
78°С |
-600°С |
-600°С |
|
Память (ширина петли
гистерезиса) |
(1-20)°С |
(0,1-3)Uoff |
(0,1-3)Uoff |
|
Диапазон изменения
поверхностного сопротивления RS |
3Ом/□-3·104Ом/□ |
(5-1010) Ом |
5Ом/□-3·1010Ом/□ |
Рассматриваемая микроэлектромеханическая система, таким образом, обладает основными свойствами сред с фазовым переходом – обратимыми изменениями комплекса свойств и гистерезисом. В то же время такая структура выгодно отличается от аналога (ФПМП в VO2) возможностями управления разностью потенциалов, более широкими диапазонами изменения параметров и температурным диапазоном работы, существенно меньшими энергией и временем переключения.
Эти важные количественные параметры дополняются рядом качественных отличий. Среди них следует отметить большое разнообразие физических и химических воздействий, вызывающих переход, энергонезависимую память в любом состоянии и возможность существования колебаний, поддерживаемых энергией физического вакуума, многовходовость и возможность локальным воздействием вызывать быстрое обратимое переключение из состояния в состояние на больших площадях. Развитие технологии создания трехмерных структур реализуется в структурах с переключениями как в плане, так и по глубине, что сообщит им новые функциональные возможности.
Микроэлектромеханическая система на основе композитной среды
Изучена возможность создания аналога среды с ФП на основе МЭМС, включающей в себя композитную среду. Между проводящими обкладками конденсатора заключена композитная среда, представляющая собой совокупность проводящих и не проводящих частиц. Примерами таких сред могут служить аэрогели. Одна из обкладок может перемещаться под действием приложенной разности потенциалов, что приводит к изменению расстояния между частицами (p) и объемной доли проводящих частиц (q). Изменения этих параметров могут приводить как к монотонному, так и к скачкообразному изменению свойств среды. По мере повышения управляющего напряжения расстояние между обкладками уменьшается, и при определенном смещении сила кулоновского притяжения превосходит силу упругости (срыв системы), что вызывает резкое уменьшение p и увеличение q. Изменение q приводит к изменению электродинамических свойств среды при постоянстве свойств компонентов, а уменьшение p может приводить к изменению самого характера композита вследствие перколяционных явлений, туннелирования и объединения разрозненных квантовых точек в среду с перекрывающимися электронными состояниями.
В данной статье основное внимание уделено выяснению зависимостей между воздействующим напряжением и изменением свойств композита в ситуации, в которой свойства компонентов и контактов между ними не зависят от y.
До и после срыва сила электростатического притяжения уравновешивается силой упругости:
|
|
(1) |
где U – прикладываемое напряжение; S – площадь управляемого электрода; d – расстояние между обкладками; y – перемещение подвижного электрода; k – коэффициент, зависящий от механических свойств композита; εc – зависящая от y комплексная диэлектрическая проницаемость композитной среды.
Для нахождения зависимости свойств среды от приложенного напряжения проведено совместное решение уравнения (1) и уравнения:
|
|
(2) |
описывающего [6,7] связь εc с диэлектрическими проницаемостями проводящих и непроводящих компонентов (ε1,ε2,ε3) с их объемными долями (q1,q2,q3) фактором деполяризации b. В уравнении (2) объемные доли компонентов являются функциями смещения y. При этом учитывалось, что объемы твердых проводящей и диэлектрической фаз неизменны, а их объемные доли являются функциями смещения подвижного электрода.
Установлено что действительная и мнимая части комплексной диэлектрической проницаемости, показатели преломления и поглощения, проводимость и волновое сопротивление среды управляются приложенным к конденсатору напряжением.
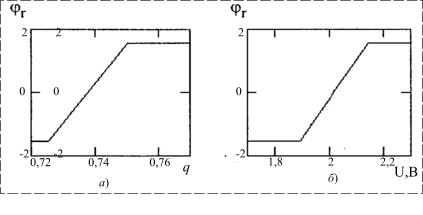
В качестве примеров на рис. 4 приведены полученные зависимости фазы φr,. отраженной волны, приведенной к начальной, от приложенного напряжения U и от объемной доли проводящих частиц q1 в зависимости от смещения y, отнесенного к начальному зазору d.
|
|
|
Рис. 4. Зависимости фазы φr отраженной волны от |
Таким образом, установлено, что в рассматриваемой МЭМС под воздействием приложенного напряжения происходит обратимое управляемое изменение комплекса свойств среды, подобное изменениям свойств при ФПМП или ФПМД.
Резонансные явления в МЭМС-аналогах сред сФП
Представляет интерес выяснение условий возникновения в рассматриваемых структурах резонансных явлений. Это важно, с одной стороны, для создания ситуаций, в которых минимальное воздействие на входе может приводить к переключению системы, а с другой – для выяснения областей параметров и воздействий, обеспечивающих заданный уровень стабильности.
Было показано [8], что кулоновская сила при включении МЭМС во внешнюю цепь
может существенно зависеть не только от амплитуды приложенного напряжения, но и
от частоты переменного сигнала и параметров внешней цепи. Установлено, что
когда рассматриваемая МЭМС включена в цепь последовательно с индуктивной
нагрузкой L, возможна ситуация, в которой в
системе без потерь сила неограниченно возрастает. В отсутствии внешнего напряжения
емкость МЭМС 
, “собственная частота” полученного последовательного
колебательного контура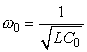 
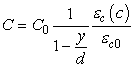, и
зависимость электростатической силы от смещения и внешних параметров (ω,U) примет вид:
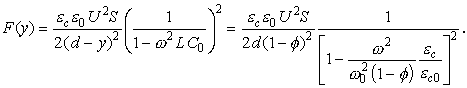
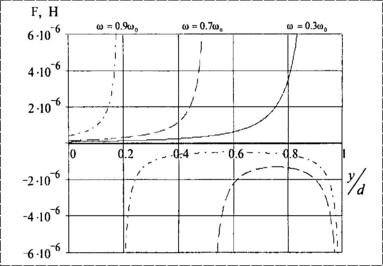
На рис. 5 приведены расчетные зависимости силы от приведенного смещения
при различных частотах внешнего электрического сигнала при
условии малой зависимости εc от y.
|
|
|
Рис. 5. Зависимости силы от приведенного |
При приближении значения отклонения y к величине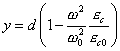 
(или при
соответствующей подстройке частоты) сила в системе без потерь неограниченно возрастает.
Следует отметить, что в системе реализуются множественные резонансы.
В композитах может наблюдаться ряд собственных резонансных явлений [9]. Так,
например, в композитах с проводящими частицами при выполнении условия 
вместо одной
плазменной частоты может наблюдаться до трех резонансных частот, при которых
действительная часть комплексного показателя преломления – ε′ проходит
через ноль (здесь ωp и τ – плазменная частота и время релаксации импульса свободных
носителей заряда соответственно). Резонансные явления в этих условиях
существенным образом зависят от объемных долей компонентов и фактора
деполяризации, определяемого формой частиц и их ориентацией относительно
электрического поля. При воздействии электрического поля в МЭМС с композитом
могут существенным образом изменяться и ориентация частиц, и их объемные доли,
что должно приводить к изменению электродинамических и оптических свойств таких
структур.
Зависимости комплексной диэлектрической проницаемости и проводимости от
параметров среды и частоты в композитах в так называемой низкочастотной
области, в которой 
, насколько можно судить по доступной литературе, практически
не исследованы. Также нет каких-либо указаний на изучение свойств композита в
МЭМС. Низкочастотная область охватывает очень широкий диапазон. В зависимости
от свойств частиц проводящей фазы его верхняя граница варьирует от 1012
до 1014 Гц. Поэтому здесь сообщаются результаты изучения
зависимостей в низкочастотной области.
Связь комплексной диэлектрической проницаемости проводящей фазы ε с ее низкочастотной проводимостью σ, временем релаксации импульса носителей заряда τ и высокочастотной диэлектрической проницаемостью εL можно записать следующим образом:
.
Для расчета свойств композита использовалась модель эффективной среды, и комплексная диэлектрическая проницаемость определялась решением уравнения, получаемого на основе (2). Расчеты проводились для двух- и трехкомпонентных сред.
|
|
|
|
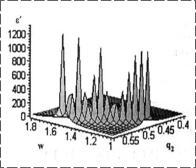
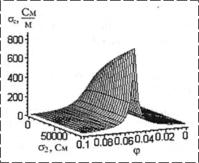
Рис. 6. Зависимость действительной |
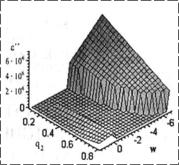
Рис. 7. Зависимость мнимой части |
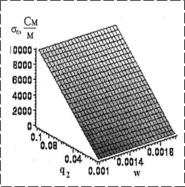
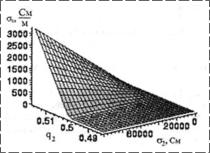
Обнаружены резонансные зависимости действительной части комплексной диэлектрической проницаемости композита ε′ от соотношения объемных долей q компонентов и фактора деполяризации и резкие изменения ε′′ от этих же параметров, что иллюстрируется рис. 6, 7.
|
|
|
|
Рис. 8. Зависимость высокочастотной |
Рис. 9. Зависимость высокочастотной |
При изменении напряжения, подаваемого на МЭМС-конденсатор с композитным
наполнением, происходит изменение q2 и может
изменяться фактор деполяризации. Независимость объема проводящей фазы от
смещения y позволяет записать 
.
|
|
|
Рис. 10. Зависимость действительной части |
Заключение
Установлена возможность создания МЭМС-аналогов сред и структур с фазовыми переходами металл-полупроводник или металл-диэлектрик на основе периодических структур и структур с композитом, в которых комплекс свойств может обратимо изменяться в зависимости от значения амплитуды или частоты поданного управляющего напряжения или механического воздействия на подвижные элементы. Варьируя управляющие параметры, можно осуществлять как монотонное, так и скачкообразное изменение комплексных диэлектрической проницаемости и показателя преломления и определяемых ими функциональных характеристик. Рассматриваемые микроэлектромеханические системы обладают основными свойствами сред с фазовым переходом – обратимыми изменениями комплекса свойств и гистерезисом. В то же время такие структуры выгодно отличаются от аналога (ФПМП в VO2) возможностями управления разностью потенциалов, более широкими диапазонами изменения параметров и температурным диапазоном работы, существенно меньшими энергией и временем переключения. Эти важные количественные параметры дополняются рядом качественных отличий. Среди них следует отметить большое разнообразие физических и химических воздействий, вызывающих переход, энергонезависимую память в любом состоянии и возможность существования колебаний, поддерживаемых энергией физического вакуума, многовходовость и возможность локальным воздействием вызывать быстрое обратимое переключение из состояния в состояние на больших площадях.
Список литературы
1. Климов Д.М., Васильев А.А., Лучинин В.В. и др. Перспективы развития микросистемной техники в XXI веке // Микросистемная техника. 1999. № 1. С. 3-6.
2. Бугаев А.А., Захарченя Б.П., Чудновский Ф.А. Фазовый переход металл-полупроводник и его применение. Л.: Наука, 1979. 183 с.
3. Casimir H.В.G., Prос. К.Ned. // Akad. Wet. 1948. Vol. 51.P. 793.
4. Мостепаненко В.В., Трунов С.Н. Эффект Казимира и его приложения // УФН. Т. 156. Вып. 3. С. 385-426.
5.
Kind H.,
Bonard J.M., Emmenegger С. et al. Patterned films of nanotubes using microcontact printing of
catalysts // Advanced Materials. 1999. 11. № 15. P. 1285-1290.
6. Bergman D. The Dielectric Constant of Composite Material // Phys. Rev. C. 1978. V. 43. № 9. P. 377-406.
7. Оделевский В.И. Расчет обобщенной проводимости гетерогенных систем // ЖТФ. 1951. Т. 21. Вып. 6. С. 667-685.
8. Биленко Д.И., Плякин М.Е., Терин Д.В. и др. Влияние электрического поля на свойства наноструктур // Вторая международная конференция “Фундаментальные проблемы физики” (ФПФ 2000). Саратов, Россия, 9-14 октября 2000 года. Материалы научной конференции. Саратов: Изд-во ГосУНЦ, 2000. 208 с.
9.
Биленко Д.И., Галишникова Ю.Н., Хасина Е.И.
и др. Электродинамические свойства полупроводниковых неупорядоченных сред //
Физика полупроводников и полупроводниковая электроника. Саратов: Изд-во Сарат.
ун-та, 1986. Вып. 12. С. 32-51.