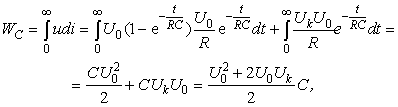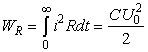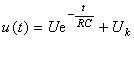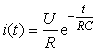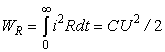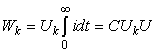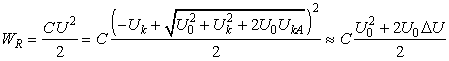УДК 621.382

В.Г.Днепровский, канд. техн. наук,

Г.Я.Карапетьян, Г.А.Пустовалов, М.В.Лысенко,

НИИ механики и прикладной математики Ростовского государственного университета, г. Ростов-на-Дону

e-mail: dnepr@math.rsu.ru

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ термоЭДС ОТ МАГНИТНОГО ПОЛЯ В ПОЛУПРОВОДНИКОВОМ КРИСТАЛЛЕ

Рассмотрены процессы зарядки и разрядки конденсатора, одна обкладка которого сделана из металла, а другая – из полупроводника, на который с внешней стороны нанесен металлический электрод. Показано, что при зарядке конденсатора в магнитном поле и разрядке, когда магнитное поле отсутствует, дополнительная потенциальная энергия конденсатора может выделиться не только на контакте металл – полупроводник, но и на резисторе, через который разряжается или заряжается конденсатор.

С появлением микроминиатюрных устройств, разрабатываемых в рамках микро- и наносистемной техники возрастает актуальность разработки микроминиатюрных источников питания длительного пользования и охлаждающих устройств для улучшения шумовых характеристик. Одной из возможных реализаций этой проблемы является использование термоэлектрических преобразователей с повышенным КПД. В настоящей работе приводятся результаты исследований, подтверждающие возможность реализации новой конструкции термоэлектрического преобразователя с высоким значением КПД.

Рассмотрим заряд термоэлектрического конденсатора, который и представляет систему металл – полупроводник – диэлектрик – металл, от постоянного источника напряжения через резистор R.

Уравнение, описывающее этот процесс, имеет вид:

,

(1)

где , С₂, С₃ – емкость между металлом и полупроводником, образованная за счет того, что электрическое поле проникает в полупроводник; C₁ – емкость межэлектродного пространства, где находится диэлектрик, u_C1=φ′₁-φ′₀, u_C2=φ’₀-φ₀, u_C3=φ₁-φ’₁ изменение потенциала на C_i. Если используется достаточно низкоомный проводник (с проводимостью более 0,1 Ом^-1·см), то глубина проникновения электрического поля в глубь полупроводника не превышает сотых долей микрометра, а толщина диэлектрической пленки выбирается в пределах нескольких микрометров, поэтому C₁«С₂ и C₁«С₃. По этой же причине u_C1pu_C2, u_C1pu_C3 и , можно записать для напряжения на конденсаторе:

(2)

Решение уравнения (2) имеет вид:

.

(3)

В начальный момент времени конденсатор не заряжен, поэтому , , поэтому u(0) = U_k, поскольку u = u_C1+u_C2+u_C3.

Тогда:

, и .

(4)

Ток через конденсатор 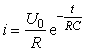, а энергия заряженного конденсатора:

(5)

где – энергия, полученная конденсатором от источника напряжения; CU₀U_k – энергия, поглощенная из окружающей среды, так как направление тока заряда выбрано таким образом, что в контакте металл – полупроводник электроны переходят из металла в полупроводник. При таком направлении тока, когда электроны переходят из металла в полупроводник, им приходится преодолевать потенциальный барьер, равный разности энергий между уровнем Ферми и дном зоны проводимости. Это могут сделать только "быстрые электроны", поэтому в контакте с избытком остаются "холодные" электроны и он охлаждается. Когда ток идет в противоположном направлении, электроны переходят из полупроводника в металл. Так как энергия электронов в полупроводнике больше, чем в металле, то они при переходе отдают часть своей энергии кристаллической решетке, и переход нагревается. Это явление называется эффектом Пельтье, а коэффициент Пельтье П равен контактной разности потенциалов [5] (П-U_k).

Энергия, выделившаяся на резисторе:

.

(6)

В [1-5] показано, что внешние поля (магнитное, электромагнитное излучение, поле механических деформаций) могут изменять термоЭДС. Поэтому U_kA=U_k+ΔU_k(A), где А – основной параметр внешнего поля (для магнитного поля – это индукции магнитного поля В, для электромагнитного излучения – интенсивность излучения на частоте максимального поглощения I, для деформаций – относительная деформация S. Например, магнитное поле изменяет соотношение быстрых и медленных электронов в токе, за счет того, что быстрые электроны рассеиваются на тепловых колебаниях кристаллической решетки меньше, чем медленные электроны, т.е. в зависимости от значения магнитного поля число быстрых электронов в токе растет, что приводит к увеличению коэффициента Пельтье П =аТ =U_k, а следовательно, и термоЭДС α=α₀[1+с_α(η_НВ)²], где α₀ – термоЭДС в отсутствии магнитного поля; с_α – коэффициент, зависящий от характера рассеяния электронов (при рассеянии на тепловых фононах с_α≈0,154), η_Н – холловская подвижность электронов в полупроводнике. Так как время рассеяния электронов на тепловых фононах – порядка 10^-11 с [4], то при каждом изменении магнитного поля новое равновесное распределение электронов установится также за это время. Это означает, что изменение α и U_k будет происходить с запаздыванием 10^-11 с, поэтому им можно пренебречь, если постоянная времени при зарядке конденсатора RCp10^-11 с.

Если термоэлектрический конденсатор при зарядке поместить во внешнее поле, то в этом случае:

.

(7)

При выносе заряженного конденсатора из внешнего поля (А=0) его энергия не изменится, так как внешние поля неэлектрического происхождения не могут изменить заряд на конденсаторе, когда он разомкнут, а предполагается, что емкость не изменяется под действием внешних полей. Например, магнитное поле не может совершить работу по зарядке конденсатора потому, что изменяющееся во времени магнитное поле (при его выключении) порождает вихревое электрическое поле, которое, в свою очередь, порождает вихревые токи только в электродах конденсатора, не изменяя их заряда.

Следовательно, при отсутствии внешнего поля (В=0) энергия конденсатора:

W_CA=0=W_CA≠0, т.е.

,

(8)

где U – напряжение на металлических электродах термоэлектрического конденсатора;

.

(9)

Нетрудно заметить, что при U₀=0, U=0, а при U₀pU_kA, U_kU ≈U₀+ΔU, ΔU =U_kA-U_k.

При разрядке конденсатора на резистор R при отсутствии магнитного поля уравнение, описывающее этот процесс, имеет вид:

.

(10)

Решение этого уравнения , а начальный момент u(0)=A+U_k=U_k+U, т.е. A=U:

и .

(11)

Энергия, которая выделится на резисторе:

.

(12)

Энергия, выделившаяся на контакте металл-полупроводник:

.

(13)

Таким образом, в контакте поглощается энергия CU_kAU₀, а выделяется CU_kU. Тогда:

.

(14)

При U₀pU_км, U_k ≈U₀+ΔU и ΔW =CU₀ΔU.

Следовательно, в контакте энергии поглотится больше, чем выделится, на величину ΔW=CU₀ΔU. Согласно закону сохранения энергии эта энергия должна выделиться на резисторе R:

.

(15)

Так как CU²₀/2 – энергия, которую получает конденсатор от источника напряжения, а W_R – энергия, которую отдает конденсатор при разрядке, то получается, что при разрядке на резисторе выделится энергии больше на величину CU₀ΔU. Это происходит потому, что в контакте при зарядке конденсатора поглощается тепловая энергия из окружающей среды (контакт охлаждается). Эта поглощенная в контакте кинетическая энергия (так как при переходе через контакт кинетическая энергия электронов увеличивается за счет поглощения тепловой энергии кристаллической решетки, что приводит к охлаждению в области контакта, а следовательно, и к поглощению тепла из окружающей среды) превращается в потенциальную энергию заряженного конденсатора, что фиксируется членом W =CU₀U_км в выражении (5).

При разряде конденсатора потенциальная энергия опять превращается в контакте в тепловую (кинетическую), но превращается не вся, а несколько меньшая часть. Оставшаяся часть должна выделиться в резисторе, поскольку вся потенциальная энергия конденсатора при разряде должна израсходоваться. Если в качестве резистора поставить электродвигатель, то оставшаяся часть этой поглощенной энергии превратится в магнитную и далее в механическую, т.е. не обязательно в тепловую, и эта часть энергии равна CU₀U_к. Очевидно, что если ΔU =0, то и не будет этой дополнительной энергии, т.е. эта энергия появляется исключительно за счет изменения U_k под действием внешнего поля. КПД такого устройства:

,

(16)

где CU₀U_км – энергия, поглощенная в контакте; СU₀U_k – энергия, выделившаяся в контакте.

Интересно отметить, что при тепловом воздействии U_k =αТ и:

,

(17)

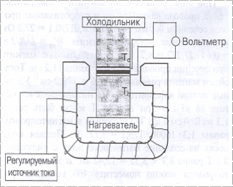
если пренебречь потерями тепла на нагревание конденсатора, т.е. КПД равен КПД цикла Карно. Для экспериментальной проверки влияния магнитного поля на термоэлектрические параметры нами был выбран кристалл антимонида индия, который имеет высокую подвижность электронов, что позволяет использовать магнитные поля с индукцией не более 0,2 Т. Как показали измерения, удельная термоЭДС α =446 мкВ/К в отсутствии магнитного поля. Образец антимонида индия выполнен в виде пластины толщиной 0,5 мм. Плоскости пластины перпендикулярны направлению (111). На эти плоскости нанесены индиевые электроды для получения антизапирающего контакта. Градиент температуры направлен перпендикулярно этим плоскостям, а вектор индукции магнитного поля направлен параллельно плоскости пластины. Схема установки показана на рисунке. При индукции магнитного поля В =0,2 Т термоЭДС увеличилась почти на 260 мкВ/К, т.е. более чем на 50%. Однако измерение коэффициента Пельтье показало, что он слабо зависит от магнитного поля (меняется не более чем на 5%). Это объясняется тем, что при помещении полупроводника в магнитное поле, индукция которого перпендикулярна градиенту температур, в нем возникает поперечная термоЭДС, пропорциональная значению индукции магнитного поля и градиенту температур. Эта термоЭДС наводит на электродах, перпендикулярных градиенту температур, ЭДС которая сильно зависит от магнитного поля. Чтобы исключить эту паразитную ЭДС проводились измерения термоЭДС при двух диаметрально противоположных направлениях индукции магнитного поля, а в качестве значения термоЭДС бралось среднее значение измеренных ЭДС. В этом случае поперечные составляющие ЭДС, измеренные при противоположных направлениях индукции магнитного поля, взаимно исключались. Тогда было установлено, что при комнатной температуре в кристаллах антимонида индия термоЭДС, как и коэффициент Пельтье, в поперечном магнитном поле с индукцией 0,2 Т изменяется не более чем на 5%.

Схема экспериментальной установки для
измерения влияния магнитного поля на термоЭДС

Для исследования временных зависимостей электроды кристалла подсоединяли к высокоомному входу осциллографа, который был засинхронизирован с генератором, создающим переменное магнитное поле. На электродах полупроводниковой пластины появлялось напряжение, обусловленное изменением контактной разности за счет изменения магнитного поля (так как термоЭДС и коэффициент Пельтье меняются с изменением магнитного поля).

Так как в диэлектрике присутствуют диэлектрические потери, то это приводит к нагреву конденсатора. Сравним мощность, которая выделяется на конденсаторе в виде теплоты, с мощностью, поглощаемой в контакте металл – полупроводник.

Для этого представим конденсатор в виде последовательно соединенных емкости С и резистора R_tgδ=tgδ/ωC, где tgδ – тангенс угла диэлектрических потерь. Мощность, выделяемая на резисторе, равна 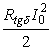. При резонансе ток I(t) и напряжение U(t) будут находиться в фазе. Тогда П_~=-βB₀×(cosω₀t)/2 и ток I(t)=I₀cos(ω₀t+φ) будут находиться в противофазе при φ=0, и I₀П_~/2 будет со знаком минус, т.е. мощность будет поглощаться, что приведет к охлаждению конденсатора. Очевидно, что охлаждение будет происходить в том случае, если мощность, выделяемая на R_tgδ, не превысит поглощаемую мощность I₀П_~/2. Тогда приравнивая эти мощности, находим предельное значение тока, превышение которого уже не приводит к охлаждению:

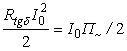, т.е.:

,

отсюда предельная плотность тока:

,

где d – толщина диэлектрической пленки. Для диэлектриков ε/tgδ≈10⁶, при ω =6,28·3·10⁴ 1/с (30 кГц) и d ≈10^-6 м (1 мкм):

.

Из выражения для j видно, что плотность тока существенно зависит от толщины диэлектрической пленки и от отношения ε/tgδ. Для П_~=0,01 B j=15 000 A/м²=1,5 A/см².

Так как магнитное поле – переменное, оно порождает вихревое электрическое поле, а следовательно, и вихревую ЭДС; E_вихр =dФ/dt =ω₀B₀S_сеч, где S_сеч – площадь конденсатора в направлении, перпендикулярном силовым линиям магнитного поля. Тогда мощность, расходуемая магнитным полем на нагревание конденсатора, W_вихр=E_вихр/R где R – сопротивление металлической пленки (как наиболее низкоомной) электрода конденсатора, R =ρ_мl/dl_ш, где l – длина, а l_ш – ширина конденсатора; S_сеч =dl, тогда:

,

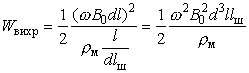где ρ_м – удельное сопротивление металла; d – толщина металлической пленки.

Мощность, поглощаемая в контакте:

.

Тогда:

.

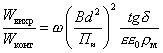При ω=6,3·10⁴ 1/с, В=0,1 Т, tgδ/ε=10^-5, П_~=10^-2В, d=10^-6 м, ρ_м=10^-8 Ом·м.

,

т.е. мощность, выделяемая в виде тепла из-за вихревых токов, на три порядка меньше мощности, поглощаемой в контакте, и ей можно пренебречь. Мощность, рассеиваемая на сопротивлении полупроводника, W_n/n=I²R_n/n. Тогда:

.

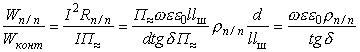При ω =6,3·10⁴ 1/с, ρ_n/n=10^-3 Ом·м, W_n/n/W_конт=55,7·10^-4, т.е. W_контpW_n/n, и потерями в полупроводнике можно пренебречь.

Рассчитаем теперь энергию, которая необходима на создание магнитного поля B(t). Прежде всего, отметим, что на изменение коэффициента Пельтье энергия не затрачивается, так как сила Лоренца перпендикулярна траектории движения электронов. Магнитное поле только перераспределяет холодные и горячие электроны в токе, оставляя их общую энергию неизменной.

Если взять магнитопровод из магнитодиэлектрика, у которого нет насыщения, сечением 16 см² и сделать там зазор l=1 см, то поле в зазоре (куда будут помещены холодильные конденсаторы) будет равно:

, где N – число витков.

При В=0,1 Т и N=1000 .

При этом, если сечение магнита – квадратное, длина провода равна 160 см и сопротивление провода сечением 0,1 мм² R=160·0,017/0,1=27,2 Ом и резистивные потери в магните W_m=I²R/2=0,64·27,2/2=8,7 Вт. Длина обмотки магнита при сечении провода в 0,1 мм равна 11,2 см. Тогда объем магнита равен 4·4·11,6=179,2 см³. Удельные потери в ферритовом магнитопроводе на частоте 16 кГц и при В =0,1 Т могут быть равны 1,3 мкВт/(см³Гц). Тогда потери в магнитопроводе равны 1,3·16 000·179,2=3,72 Вт. Полная мощность на создание магнитного поля с индукцией 0,1 Т равна 8,7+3,32=12,42 Вт. В зазоре магнитопровода можно поместить 400 конденсаторов толщиной 0,1 мм, так что поглощаемая мощность при П_~=0,01 В равна 0,01·400·4/2=8 Вт. Чтобы поглощаемая мощность превысила потери в магните, толщина конденсатора должна быть сделана в 1,5 раза меньше, т.е. должна быть не более 0,066 мм. Если магнит делать из высокотемпературного сверхпроводника, то для получения индукции магнитного поля В=0,1 Т при N =1000 и сечении провода 0,1 мм ток должен быть равен 9 А. Потери в сверхпроводящем магните отсутствуют. Поэтому на создание магнитного поля не требуется энергии. Кроме того, конденсаторы в этом случае помещают внутри соленоида, образующего сверхпроводящий магнит.

Переменное магнитное поле можно также создать с помощью постоянных магнитов, движущихся около термоэлектрических конденсаторов. В этом случае затраты энергии на создание переменного магнитного поля будут определяться только добротностью механической системы, создающей движение магнитов, т.е. трением. При использовании подшипников эти потери будут близки к нулю.

Работа выполнена в рамках проекта подпрограммы "Электроника". Код проекта: 208.06.01/№ 107.

Список литературы

1. Юри P. (Ure Ronald W.) Теория материалов для термоэлектрических и термомагнитных приборов // ТНИЭР. Т. 51. 1963. № 5. С. 702-717.

2. Гаджилаев М.М. ТермоЭДС InSb в поперечном квантующем магнитном поле // Известия вузов. Сер. Физика. № 3. 1993.

3. Гаджилаев М.М. ТермоЭДС n-InSb в поперечном магнитном поле и при большом градиенте температуры // ФТП. Т. 34. 2000. Вып. 5.

4. Уэдлок. Термофотоэлектрическое преобразование энергии // ТИИЭР. Т. 51. С. 697-702.

5. Карапетьян Г.Я., Катаев В.Ф., Ратушный В.И., Сысоев И.А. Влияние магнитного поля на величину термоЭДС в полупроводниках // Труды Международной научно-технической конференции. "Машиностроение и техносфера на рубеже XXI века". 11-17 сентября 2000 г., г. Севастополь. С. 34-35.