В.И. Волчихин, канд. техн. наук, проф., А.И. Воячек,
канд. техн. наук, доц.,
В.В. Смогунов, д-р техн. наук, проф., Пензенский
государственный университет
МОДЕЛЬ ГЕТЕРОГЕННЫХ СТРУКТУР МИКРОСИСТЕМНОЙ ТЕХНИКИ
|
Рассмотрены принципы моделирования контактных систем микросистемной техники. Приведены методики расчета и результаты исследований упругих и теплофизических характеристик контактных систем. |
Микросистемы представляют собой сложные гетерогенные структуры, требующие сочетания совокупности разнородных материалов, которые должны надежно функционировать при динамическом и температурном воздействии, в условиях агрессивности сред и радиации [1]. Одной из важных гетерогенных структур является контактная система, определяющая взаимодействие деталей и фаз в микросистемной технике.
Контактную систему можно определить как совокупность взаимно сопряженных деталей (материалов), обладающую свойством целостности, возникающим вследствие связей контактного взаимодействия. Контактные системы в микросистемной технике можно разделить на две принципиально различные группы [2]:
· контактные системы, в которых взаимодействие деталей осуществляется через шероховатые поверхности;
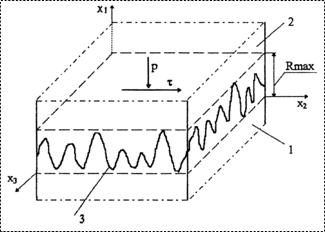
· соединения разнородных материалов, когда один из материалов заполняет полностью или частично впадины шероховатой поверхности детали, изготовленной из другого материала (см. рис. 1).
|
|
| Контактная система микросистемной техники: |
В настоящее время накоплен определенный материал для контактных систем первой группы по исследованию деформационных и теплофизических процессов, износостойкости, проводимости и т.д. Эти исследования в большинстве своем базируются на теории Герца о взаимодействии твердых тел. В то же время до сих пор не уделяется должного внимания контактным системам второй группы, хотя в некоторых микросистемах они составляют большинство. Непосредственное использование результатов, основанных на решении задачи Герца, недопустимо, так как в контактных системах второй группы гипотезы теории Герца не выполняются.
Широкое распространение контактных систем второй группы в микросистемной технике обусловлено технологиями их создания. Большинство этих технологий направлено на реализацию фазового перехода (выделение твердой фазы тем или иным способом из жидкой или газообразной фазы или травление твердой фазы) на шероховатой поверхности элемента. Таким образом, взаимодействие фаз в контактных системах второй группы осуществляется по случайной поверхности, а работоспособность их будет определяться в основном процессами, протекающими в пределах высоты шероховатостей.
В основном теорий процессов, протекающих в гетерогенном слое контактных систем второй группы, может быть положена полидисперсная модель гетерогенного материала. Полидисперсная модель предполагает изотропию свойств в плоскости системы. Согласно этой модели, упругие и теплофизические свойства гетерогенного слоя определяются следующими тензорами:
· тензор модулей упругости
;
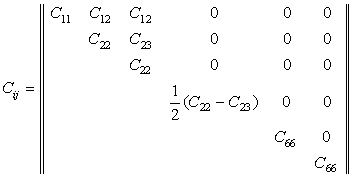(1)
· тензор коэффициентов теплопроводности
;
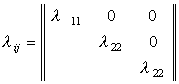(2)
· тензор коэффициентов линейного расширения
.
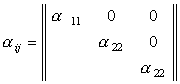(3)
В качестве примера приведем
технические эффективные модули упругости, характеризующие упругие свойства при
сжатии 
и сдвиге в плоскости контактной системы
:
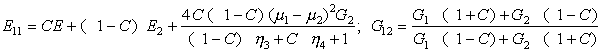, (4)
где
; 
;
, 
, 
-
модули Юнга, сдвига, коэффициенты Пуассона для первого (
) и второго (
)
материалов системы соответственно; 
- доля площади сечения,
перпендикулярного оси 
, занятая первым материалом.
В формулах (4) предполагается, что фазы являются однородными и изотропными. Вместе с тем, в результате изменения процентного содержания фаз по толщине слоя системы, гетерогенный слой в целом будет анизотропным и неоднородным.
Учитывая, что процентное содержание фаз по высоте гетерогенного слоя меняется, для его определения целесообразно использовать формулы для относительной площади опорной поверхности профиля. В случае, когда случайное поле контакта фаз подчиняется закону Грама-Шарлье и это распределение является однородным и изотропным, была получена следующая формула для относительной площади опорной поверхности:
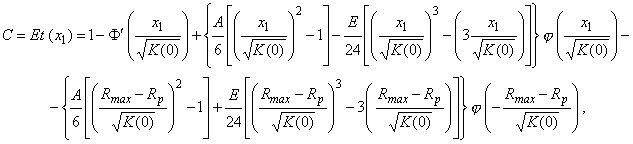(5)
где
; 
;
; 
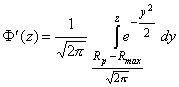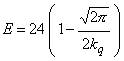– относительная
опорная площадь на уровне базовой плоскости; 
– отношение
среднего геометрического отклонения точек поля (
) к среднему
арифметическому отклонению точек поля (
); 
-
наибольшая высота неровностей профиля; 
– наибольшая
высота выступа профиля над базовой плоскостью; 
– корреляционная
функция (
).
Если в (5) положить
, то 
. Это
значение соответствует для нормального закона распределения. Поэтому при значениях
близких к 1,25, можно с достаточной
для практики точностью использовать только два члена ряда закона Грама-Шарлье.
Наряду
с эффективными показателями упругих свойств, которые характеризуют их в каждой
точке контактной системы, представляют практический интерес интегральные показатели,
характеризующие свойства системы в целом. Под интегральными показателями упругих
свойств контактных систем понимаются коэффициенты нормальной (
) и тангенциальной (
) податливости,
которые оценивают нормальную и тангенциальную жесткость системы в целом. Зависимость
между деформациями системы и действующими на них нагрузками имеет вид:
, (6)
где
, 
–
контактное давление и удельная тангенциальная сила; 
, 
–
перемещения верхней плоскости системы относительно нижней вдоль осей 
,
соответственно (см. рисунок). Выражения
для коэффициентов нормальной и тангенциальной податливости имеют вид:
.
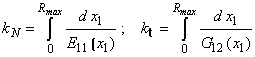(7)
Исследование упругих свойств контактных систем по приведенным
выше формулам показало, что распределение 
, 
по
толщине системы изменяется от соответствующих значений одной фазы до соответствующих
значений другой фазы, причем характер этого изменения соответствует характеру
изменения процентного содержания фаз по толщине системы. Особенно это касается
модуля 
, т.е. того модуля, формулы расчета которого в большей степени
подчиняются правилу "смеси".
Исследование коэффициентов
нормальной и тангенциальной податливости контактной системы показало, что их значение
существенно зависит от толщины системы (), модулей упругости фаз и распределения
фаз по толщине системы. Если шероховатость подчиняется нормальному закону распределения,
для которого можно принять 
; 
,
то коэффициенты нормальной и тангенциальной податливости можно представить в виде:
, (8)
где
.
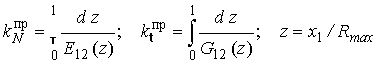В
(8) приведенные коэффициенты нормальной (
)
и тангенциальной (
) податливости зависят только от модулей
упругости фаз.
* * *
Таким образом, предложенная модель деформирования контактных систем второй группы микросистемной техники позволяет оценить среднее напряженное состояние в каждой точке системы с учетом технологии обработки поверхностей и технологий получения систем. Кроме того, получены интегральные характеристики жесткости контактных систем, введение которых в существующие методики расчета гетерогенных элементов микросистемной техники позволяет учесть особенности деформирования зоны контакта соединений разнородных материалов, обусловленные техническими особенностями производства.
Список литературы
1. Климов Д.М., Васильев А.А., Лучинин В.В., Мальцев П.П. Перспективы развития микросистемной техники в 21 веке // Микросистемная техника,1999.№ 1. С.3-6.
2. Иванов В.А., Волчихин В.И., Гордин Г.Т. Ударостойкие и виброустойчивые резистивные устройства для автономных систем управления // Организация производства и прогрессивная технология в приборостроении, 1989. № 4. С. 32-35.