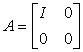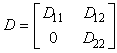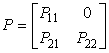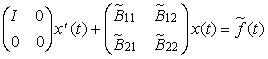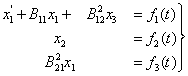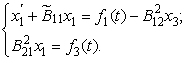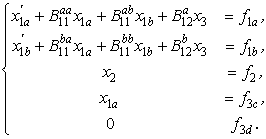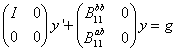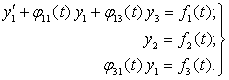УДК 512.628.2

E.В.Новожилов,
Московский Государственный Университет им. М.В.Ломоносова Факультет Вычислительной Математики и Кибернетики

О ПРИВЕДЕНИИ К ПРОСТЕЙШЕМУ ВИДУ ДИФФЕРЕНЦИАЛЬНО-АЛГЕБРАИЧЕСКИХ СИСТЕМ ДЛЯ РАСЧЕТА ЭЛЕКТРОННЫХ ЦЕПЕЙ

Рассматриваются системы линейных дифференциально-алгебраических уравнений с переменными коэффициентами, удовлетворяющими специальным условиям постоянства ранга. Системы данного типа возникают, в частности, при решении таких прикладных задач, как моделирование электронных цепей, химических реакций (определенного типа), а также задачи расчета динамики различных транспортных систем (в том числе на макроуровне). Предлагается метод приведения таких систем к определенной простейшей форме, основанный на построении итерационной процедуры. Предложенный метод применим для систем с любым значением индекса, и может быть использован для численного решения дифференциально-алгебраических систем при моделировании процессов в перечисленных прикладных задачах

Введение 1

Пример 2

Рассматриваемые системы 3

Используемые преобразования 5

Упрощение системы 5

Заключение 12

Введение

В современных методах расчета моделируемых электронных цепей [1]-[3] наиболее часто используется метод узлового анализа зарядов [4], [5]. Однако такой метод имеет один существенный недостаток: коэффициенты возникающих при этом дифференциально-алгебраических уравнений обладают недостаточной гладкостью. Индекс¹ таких систем может быть равен 2 и при этом системы могут не иметь нормальной формы Хессенберга (Hessenberg F.) [6]. Метод узлового анализа зарядов электронных цепей приводит к системам вида:

;

,

где вектор неизвестной функции (х,q) содержит:

· потенциал и узлов цепи;

· силу тока I элементов цепи с управляемым напряжением;

· заряд конденсаторов Q;

· магнитный поток Ф катушек индуктивности.

Предполагаем, что электронная цепь содержит динамические элементы: элементы емкостного сопротивления (конденсаторы) и катушки индуктивности. Для примера рассмотрим модель электронной цепи одного из наиболее распространенных элементов в интегральных схемах – логического элемента "И – НЕ" (NAND-gate).

Пример

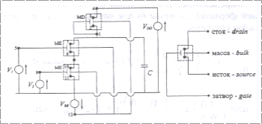
Элемент "И-НЕ" состоит из двух обогащенных МОП-транзисторов с каналом n-типа (ME), одного ослабленного (обедненного) МОП-транзистора с каналом n-типа (MD) и заряженного конденсатора (С) (рис. 1). МОП-схемы, как правило, не содержат других элементов кроме МОП-транзисторов, которые могут также выполнять функцию управляемых резисторов. В нашем примере таковым является обедненный МОП-транзистор (MD), для этой цели в его схеме соединены затвор и исток.

Рис. 1. Элемент "И – НЕ" и схема МОП-транзистора

Напряжение на стоке d(drain) транзистора MD равно V_DD = 5 В. Массы b(bulk) транзисторов не заземлены и V_BB = ‑2,5 В. Истоки s (source) обоих транзисторов ME заземлены, напряжение на их затворах g(gate) соответственно равно V₁ и V₂. Более подробная (точнее отражающая физическую структуру) схема МОП-транзистора дана в работе [5]. При расчете этой модели будет получена система с индексом 2.

Работу транзистора в соответствии с приведенной схемой можно описать так. Ток i_ds может протекать от стока к истоку тогда и только тогда, когда управляющее напряжение U_gs между затвором и истоком больше, чем пороговое напряжение (значение которого зависит от конкретной применяемой технологии) U_T. Затвор изолирован от канала сток-исток тонким слоем двуоксида кремния (SiO₂); т.е. сопротивление R_sd между истоком и стоком почти "бесконечно" большая величина (~10¹⁵ Ом).

При использовании метода узлового анализа зарядов в результате расчета получаем системы дифференциально-алгебраических уравнений с размерностью коэффициентов 29×29 (эту систему можно получить, если записать закон Кирхгофа для каждого из двенадцати узлов, обозначенных на схеме элемента). Не будем выписывать здесь все уравнения системы (система полностью приведена и рассмотрена в работе [1]), запишем только по одному уравнению (в качестве типового) из трех основных частей системы.

1. Дифференциальная часть системы – 12 уравнений для значений зарядов; одно из уравнений дифференциальной части имеет вид:

.

2. Четыре характеристических уравнения для напряжений истоков типа:

.

3. Для емкостей – 13 характеристических уравнений типа:

.

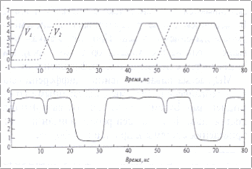
В результате моделирования с использованием, например, метода обратного дифференцирования (BDF) исходной системы можно получить следующую зависимость выходного сигнала в узле и от значений напряжения на входах V₁, V₂ (рис. 2). Значение u₁ мало (FALSE) тогда и только тогда, когда V₁ и V₂ имеют наибольшее значение (TRUE). На рисунке изображены численные результаты моделирования. Например, можно видеть, что отрезки времени [10 нс, 15 нс] и [50 нс, 55 нс] являются критическими при оценке уровня напряжения. И поэтому при установке порогового напряжения необходимо учитывать разницу двумя минимальными значениями:

· локального минимума в точках (12,5+40n) нс;

· почти постоянного минимального значения на отрезках [(25+40n) нс, (30+40n) нc].

Задача по упрощению систем дифференциально-алгебраических уравнений для расчета даже такого простого элемента электронной цепи имеет важное значение, поскольку позволяет уменьшить дифференциальную часть без изменения степени гладкости коэффициентов. В качестве объекта упрощения выберем общий вид линейной системы.

Рассматриваемые системы

Рассматриваются системы линейных дифференциально-алгебраических уравнений. Напомним, что дифференциально-алгебраической системой называется система уравнений вида [11]:

,

(1)

где A(t), B(t) – коэффициенты, зависящие от переменной tÎSÌ.

Рис. 2. Выходной сигнал в узле 1

Старший коэффициент А(t) системы (1) является, вообще говоря, вырожденным, т.е. соответствующая матрица вырождена. Поэтому система (1) может содержать и чисто алгебраические уравнения.

Основной задачей, которой посвящена данная статья, является задача о приведении системы дифференциально-алгебраических уравнений к простейшему виду, т.е. к виду, при котором система содержит минимальное число дифференциальных уравнений.

Простейшим случаем систем указанного типа является случай систем с постоянными коэффициентами. Наиболее известные [12] из уже существующих методов исследования систем с постоянными коэффициентами – это методы, связанные с приведением системы к нормальной форме Кронекера, а также метод, в котором используется так называемый проектор Дрезина и спектральные проекторы. В ином подходе [13] для упрощения системы используется разбиение с помощью специальной последовательности проекторов, называемой цепным проектором. В работе [14] для упрощения систем был предложен специальный метод выбора последовательности проекторов (канонические проекторы). В работе [15] этот метод был усовершенствован. А именно, оказалось, что при выполнении определенных условий, накладываемых на коэффициенты, исходная система может быть сведена к нормальной форме Кронекера с нильпотентной цепной матрицей Жордана в качестве коэффициента при производной в одной из двух получающихся подсистем.

Приведение к нормальной форме Кронекера позволяет разделить исходную систему на две подсистемы: дифференциальную, разрешенную относительно производной неизвестной функции, и дифференциальную, разрешенную относительно самой функции. Но при этом общее число дифференциальных уравнений не уменьшается.

Отметим также, что в перечисленных работах рассматриваются системы только с индексом 1 или 2. В настоящей статье рассматриваются системы с любым значением индекса 2. При этом все указанные выше методы не дают удовлетворительного результата для систем с переменными коэффициентами.

Мы рассматриваем линейные дифференциально-алгебраические системы с переменными коэффициентами. Будем требовать, чтобы ранг A(t) был постоянным. В настоящей работе описан процесс приведения системы к простейшей форме.

Определение. Простейшим видом (или простейшей формой) системы будем называть один из двух видов системы:

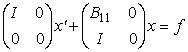(1-я простейшая форма),

или 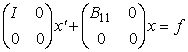(2-я простейшая форма),

где В₁₁ – некоторая матрица, зависящая, вообще говоря, от переменной t.

Здесь и далее в этой работе под словами упрощение системы будем понимать приведение системы к простейшему виду, указанному в данном определении, а под словами упрощение матрицы – приведение матрицы к виду .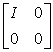

Ниже мы перечислим преобразования, которые используются для упрощения системы, после чего опишем общую итерационную схему и затем построим итерационную процедуру по указанной схеме, подробно описав каждый шаг.

Используемые преобразования

Будем рассматривать класс линейных систем с постоянным рангом. А именно, рассматриваем системы вида:

,

где , , tS, E₁, E₂ – некоторые линейные пространства:

,

зависящие от t гомоморфизмы линейных пространств, для которых выполнено условие 3 rankA(t)=const.

Сведение системы к простейшему виду осуществляется двумя типами преобразований. Первый тип – умножение системы слева на невырожденную матрицу D. Это преобразование можно рассматривать, как преобразование в пространстве Е₂. При этом система:

переходит в систему:

.

Второй тип – преобразование в пространстве E₁. При этом система переходит в систему:

.

Здесь D(t) и P(t) автоморфизмы пространств Е₁ и Е₂. Попытаемся теперь с помощью конечного числа таких преобразований выделить дифференциальную часть в нашей системе (1). Преобразование системы с помощью D(t) и P(t) можно описать в виде следующей диаграммы:

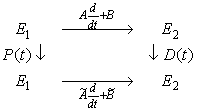
Упрощение системы

Опишем последовательность шагов по приведению системы к простейшей форме.

1. Сначала упрощаем матрицу A(t) (приводим к виду ). Это делается достаточно просто (см. ниже).

2. Далее преобразуем коэффициент B(t) для приведения его к виду, указанному в определении простейшего вида системы. При этом, вообще говоря, мы уменьшаем размерность системы (исключая получившиеся алгебраические уравнения, разрешенные относительно компонент вектора решения и условия согласования на значения правых частей исходной системы).

Преобразование матрицы B(t) является более сложной процедурой и будет проводиться по некоторой итерационной схеме.

Итак, сначала упрощаем коэффициент А. Именно с помощью преобразований D(t) и P(t) сводим этот коэффициент к виду:

.

(2)

Это можно сделать благодаря тому, что (по условию) матрица А имеет постоянный ранг. Применение преобразований D(t), P(t) к исходной системе, приводит ее к виду:

,

(3)

где 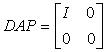. Здесь для простоты аргумент t у матриц D, Р, А, В опущен и через 7 обозначено новое (преобразованное) значение правой части.

Далее нам необходимо привести коэффициент В к достаточно простому виду. И поскольку теперь в ходе дальнейших преобразований нужно сохранять канонический вид (2) коэффициента А, то преобразования D, P должны иметь специальную форму, а именно:

,

(4)

причем D₁₁P₁₁=1, а матрицы D₂₂ и Р₂₂ – произвольные и обратимые.

Такая структура и размерность матриц D и Р соответствуют разбиению пространства Е₁ на подпространства E₁₁, E₁₂ и пространства Е₂ на подпространства Е₂₁, Е₂₂:

, ,

где:

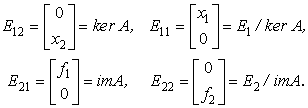
При этом получается, что:

Система (3) после преобразований (4) приобретает вид:

,

(5)

где:

;

;

;

(6)

;

.

Для упрощения записи вернемся снова к обозначению В вместо и к f вместо , имея в виду уже преобразованные значения.

Теперь применяем итерационную процедуру по упрощению матрицы В.

1-й итерационный шаг

Сначала приводим элемент В₂₂ коэффициента В к виду:

.

(7)

Это можно сделать аналогично тому, как мы упрощали матрицу А, естественно при условии:

(8)

Сформулируем это условие в терминах исходных коэффициентов А и В. Заметим, что В₂₂ действует в пространствах Е₁₂, Е₂₂, или, в других обозначениях:

,

(В₂₂= В|kerA).

Тогда условие (8) можно записать следующим образом:

.

После приведения матрицы В₂₂ к виду (7) и нескольких дополнительных элементарных преобразований получаем систему (с естественными обозначениями):

.

(9)

При этом для переменной х₂ получаем точное выражение:

.

Рассмотрим теперь два оставшихся уравнения:

(10)

Независимо от значения коэффициента В²₁₂ компонента х₃ вектора решения выбирается произвольно, a x₁ есть решение дифференциального уравнения, которое должно удовлетворять условию B²₂₁x₁=f₃(t). Поэтому решение такой задачи возможно не при любых значениях f_i в правой части. И на следующих этапах преобразований будут появляться дополнительные условия согласования. Следующим этапом итерационного шага является приведение⁴ блока B²₂₁ к виду:

.

(11)

И здесь очевидно необходимо наложить следующее условие постоянства ранга:

.

Заметим, что B²₂₁ – это матрица отображения , действие которого можно описать с помощью следующей диаграммы:

.

Оператор В₂₂=В|_kerA определен ранее.

Для упрощения В₂₁ мы используем преобразования, которые не только сохраняют нормальную форму А, но и текущую форму В. Нетрудно видеть, что эти преобразования D и Р должны иметь такую форму:

, ,

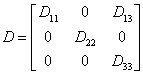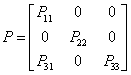и удовлетворять условиям:

(матрицы D₃₃ и Р₁₁ обратимы). Посмотрим, к какому виду мы сведем систему. Представим элементы x₁, f₁, f₃ каждый в виде двух векторов:

, , .

Тогда полученная система запишется в виде:

(12)

Теперь подставим значение x_1a в первое уравнение и в результате получим:

1) новую дифференциально-алгебраическую систему относительно переменной x_1b :

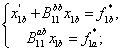
2) условие согласования для правой части:

;

3) несколько алгебраических уравнений, из которых однозначно определяются некоторые компоненты решения:

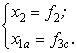
Введя обозначения:

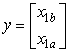и ,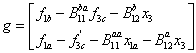

получим новую систему:

.

(13)

Таким образом, после первого шага итерации мы пришли к системе, в которой главный коэффициент А имеет требуемую каноническую форму , и при этом уменьшили количество дифференциальных уравнений в системе. На этом заканчивается 1-й итерационный шаг.

2-й итерационный шаг

Будем упрощать коэффициент 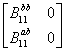по уже рассмотренной итерационной процедуре, в которой каждый следующий шаг итерации начинается с упрощения блока⁵ В₂₂, приводя его к виду или, если В₂₂ =0, как в данном случае, с упрощения блока В²₂₁. Например, в системе (13) этому блоку отвечает блок В^ab₂₁, который и будем приводить к простому виду. При этом, естественно, надо потребовать, чтобы:

.

(14)

Заметим, что В^ab₁₁ – это матрица отображения, действие которого можно представить с помощью следующей диаграммы:

.

Сделаем важное замечание. В процессе приведения системы к простейшей форме мы последовательно разбиваем исходную матрицу коэффициента B системы (1) на подматрицы:

· сначала (после упрощения матрицы А) в (5) на подматрицы В₁₁, В₁₂, В₂₁, В₂₂;

· затем (после приведения B₂₂ к виду (7)) в свою очередь разбиваются B₁₂ (на нулевую подматрицу и подматрицу B²₁₂) и B₂₁ (на нулевую подматрицу и подматрицу В²₂₁).

И с этого момента до последнего шага итерации мы последовательно разбиваем на подматрицы блок В₁₁ системы (5). Сначала, например, после приведения В₂₁ к виду (11) В₁₁ разбивается на подматрицы B^aa₁₁, B^ab₁₁, B^ba₁₁, B^bb₁₁ так, что dimB^aa₁₁=rankВ²₂₁, и так далее. Запишем эту последовательность разбиения в виде схемы (используя другие индексы для подматриц):

B11→		B01	B02			,	(15)
		B03	B11	B12
			B13	B21	B22
				B23

где в принятых обозначениях, например, В₀₂ соответствует B^ab₁₁ в системе (12). Разбиение при этом осуществляется так, что:

.

Например, dimB₁₁ = rankB₀₂. Очевидно, что итерация заканчивается тогда, когда:

,

и (m+2)-й шаг будет последним шагом итерации. В диаграмме (15) выделением отмечены те блоки, постоянства рангов которых мы будем требовать на соответствующих шагах итерации. Если усилить эти условия и потребовать, чтобы:

,

(16)

то для сведения системы (1) к простейшему виду условие (16) будет достаточным, но не будет необходимым.

Завершение итерации

Итерационная процедура заканчивается на m-м шаге, где m такое, что В_(m-2)2 =0 или B_(m-2)2=I. При этом все оставшиеся дифференциальные и алгебраические уравнения в исходной системе будут сведены либо к условиям согласования на значения правых частей:

,

либо к алгебраическим уравнениям вида:

.

Систему на этом последнем шаге итерационного процесса будем называть финальной системой.

Таким образом, мы доказали следующую теорему.

Теорема. Произвольная линейная дифференциально-алгебраическая система типа (1) может быть сведена к простейшему виду, если коэффициенты А и В этой системы удовлетворяют следующим условиям:

1);

2);

3);

4).

Следствие. Из условий, сформулированных в теореме, можно сделать следующие выводы:

· условия 1, 2 и 3 являются необходимыми и достаточными для сведения системы, к виду (13);

· чтобы сформулировать необходимые и достаточные условия, надо ослабить условие 4, а именно, потребовать выполнения условий rankВ_i2=const, где i =0,1,...,m; m: rankB_(m-1)2=rankB_((m)2).

Пример. Рассмотрим пример конкретной системы и покажем, к какому результату можно придти в ходе упрощения по построенной выше итерационной схеме. Пусть исходная система имеет вид:

(17)

Все компоненты x₁, х₂, х₃ – скаляры. Как видно из системы (17), коэффициент А уже имеет каноническую форму, коэффициент В тоже имеет простой вид в соответствии с итерационной схемой. Поэтому в ходе упрощения и решения такой системы нам не потребуется проделывать все этапы (кроме последнего) на 1-м шаге итерации. Результат упрощения будет следующим:

а) если φ₃₁=0, то имеем финальную систему вида:

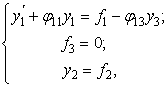
где f₃ =0 – условие согласования; y₃ – выбирается произвольно; у₁=y₁(t,С) – решение дифференциального уравнения;

б) если φ₃₁≠0, то при φ₁₃=0 получим систему, в которой будет только два алгебраических уравнения и одно условие согласования, а дифференциальная часть будет полностью отсутствовать:

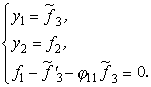
Наконец, при φ₁₃≠0 все компоненты решения определяются однозначно:

.

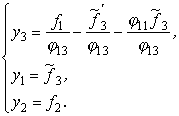Заключение

Наиболее часто решение дифференциально-алгебраических систем (с переменными или постоянными коэффициентами) большой размерности необходимо при расчете, анализе и реконструировании фрагментов моделируемых электронных цепей (а также систем электронных цепей в целом). Метод, предложенный в настоящей работе, формализует процесс упрощения дифференциально-алгебраических систем. В этом методе используются не только линейные подстановки компонентов решения, которые обычно составляют основную часть циклов методов численного решения таких систем (например, методы Рунге-Кутта), но и дифференциальные подстановки. Это, в свою очередь, позволяет уменьшить количество дифференциальных уравнений в системе. Предложенный метод может быть использован в качестве алгоритма для численного решения задачи по упрощению.

В настоящей работе рассматривались системы дифференциально-алгебраических уравнений следующего типа:

,

с накладываемыми на коэффициенты A(t) и B(t) системы условиями rankA=const, rank(В|_kerА)=const, rankВ|_[E3/kerA]=const, rankВ|^аb₁₁=const.

Был предложен способ упрощения системы – получения простейшей формы, т.е. такого вида системы, при котором она, во-первых, имеет наименьшее количество дифференциальных уравнений, и во-вторых, матрица B имеет вид:

, или .

В данном методе использована специальная итерационная процедура преобразования матрицы В. Итерация заканчивается тогда, когда мы приходим к финальной системе. Еще раз отметим тот факт, что предложенная схема применима для дифференциально-алгебраических систем с любым значением индекса.

Автор статьи выражает большую признательность и благодарность профессору Виктору Евгеньевичу Шаталову за ценные советы и оказанную помощь в работе над статьей.

¹Число последовательных операций дифференцирования для сведения к простейшей форме.

²Здесь под индексом понимается число, характеризующее количество формальных операций дифференцирования, необходимых для редукции системы к некоторому простому виду.

³В дальнейшем (при описании итерационной процедуры) мы наложим также дополнительные условия постоянства ранга.

⁴Если на некотором шаге итерации блок B²₂₁=0, то это означает конец итерационного процесса.

⁵Мы используем введенные выше обозначения для элементов матрицы коэффициента при алгебраической части системы.

Список литературы

1. Tischendorf С., Marz R. Recent results in solving differential-algebraic equations in circuit simulation // SIAM Journal. Scientific Computation. 1997. 18 (1): 139-159.

2. Марьяшкин Н.Я., Овчинников Е.Э., Белаш В.О., Глебов А.Л. Решение дифференциально-алгебраических систем схемотехнического анализа БИС. М.: ВЦ АН СССР, 1991.

3. Нерретер В. Расчет электрических цепей на персональной ЭВМ. М.: Энергоатомиздат, 1991.

4. Tischendorf С. Solution of Index-2 Differential Algebraic Equations and its Application in Circuit Simulation. Дис., 1994.

5. Günther M., Feldman U. CAD-modelling of electric circuits. A classification with respect to structure and index. 1995. (рукопись).

6. Griepentrog E. Index reduction methods for differential-algebraic equations // Inst. fur Mathem. Берлин: Humboldt-Univ. 1992. 92-1, P. 14-29.

7. Gear G.W. Differential-algebraic equations index transformations // SIAM J. Sci. Stat. Comput. 1993. 9: 39-47.

8. Gear G.W. The simultaneous numerical solution of differential-algebraic equations // IEEE Trans. Circuit Theory. CT-18. 1971. P. 89-95.

9. Gear G.W., Petzold L. R. ODE methods for the solution of differential-algebraic systems // SIAM J. Num. Anal. 1984. 21 (4). P. 716-728.

10. Brenan K.E., Campbell S.L., Petzold L.R. Numerical solution of initial value problems in differential-algebraic equations. Elviser Science Publishing Co. Inc., 1989.

11. März R., Griepentrog E. Differential-algebraic equations and their numerical treatment // Teubner Texte zur Mathematik. 1986. 88. Leipzig. Teubner.

12. Lewis F.L. A survey of linear singular systems // Circuits Systems Signal Process. 1986. 5 (1): 3-36.

13. März R., Griepentrog E. Basic properties of some differential-algebraic equations // Zeitschrift fur Analysis und ihre Anwendungen. 1989. 8 (1): 25-40.

14. März R. On quasilinear index-2 differential-algebraic equations // Fachbereich Mathematik, 1992.

15. März R. Canonical projectors for linear differential-algebraic equations // Computers Math. Aplic. 1996. 31 (4).

16. Шубин Е.А., Егоров А.Е. Линейные дифференциальные уравнения в частных производных // Современные проблемы математики: фундаментальные исследования. Т. 30. М.: ВИНИТИ, 1987.

17. Шабат Б.В., Лаврентьев М.А Методы теории функции комплексного переменного. М.: Наука, Изд. 4, 1973.

18. Михлин С.Г. Линейные уравнения в частных производных. М.: Наука, 1977.

19. Hansen В. Linear differential-algebraic equations // Fachbereich Mathematik. Humboldt-Univ., 1992. 92-1. P. 30-38.

20. März R. Extra-ordinary differential-algebraic equations. Attempts to analysis of differential-algebraic systems // Fachbereich Mathematik. 1997. (93-13).

21. Winkle R., Lamour R., März R. How floquet theory applies to differential-algebraic equations // Journal of mathematical analysis and applications. 1996. 217: 372-394.

22. März R. Criteria for the trivial solution of differential-algebraic equations with small nonlinearities to be asymptotically stable // Fachbereich Mathematik. 1997. (97-13).

23. März R., Balla K. Transfer of boundary value conditions for daes of index-1 // SIAM Journal. Numerical Analysis. 1996. 33 (6): 2318-2322.

24. Shatalov V.Ye., Sternin B.Yu. Borel-Laplace Transform and Asymptotic Theory (Introduction to Ressurgent Analysis) // CRC-Press, 1995.

25. Левинсон Н., Коддингтон Э.А. Теория обыкновенных дифференциальных уравнений. М.: Изд-во иностранной литературы, 1958.